第4回 免震の弱点

はじめに

今回は、意外に知られていない免震の弱点についてお話しします。

それは、免震は脆いということです。

もちろん、使い方を誤らなければ免震は安全です。

特異な地震応答性状

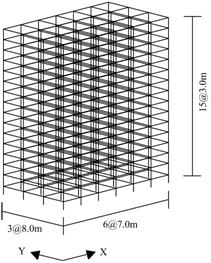
【図4.1】のようなRC造15階建ての建物を、基礎固定と免震で2通りに設計してみました。

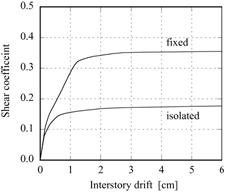
建物の静的増分解析結果は【図4.2】の通りです。

グラフの縦軸はベースシアー係数です。

基礎固定（fixed）ではC₀=0.3、免震（isolated）ではC₀=0.15くらいの保有耐力となっており、両者とも現実的な値です。

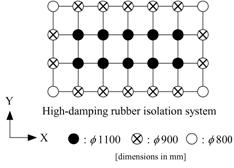
免震システムは高減衰積層ゴムを想定しました。

入力地震動を建築センター波（BCJ-L2）とし、その最大加速度を25Galずつ増やして25Galから750Galの範囲で30ケースの地震応答解析を行いました。

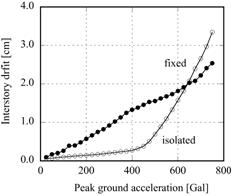
【図4.3】は入力地震動の最大加速度と建物1階の層間変形の関係を示しています。

入力レベルを上げると層間変形が増える状況はどちらも同じですが、層間変形の増え方が基礎固定と免震では大きく異なります。

基礎固定は原点からほぼ直線的に増えていくのに対して、免震では入力地震動の最大加速度が400Galあたりから急激に層間変形が増え始め、600Galを超えると逆転してしまいます。

免震の設計では、建築センター波（BCJ-L2）を拡幅して用いることは通常ありません。

BCJ-L2原波の最大加速度は356Galであり、その付近での層間変形を見ると、免震の応答は基礎固定のそれの半分以下であり、十分に免震効果は発揮されています。

免震において層間変形が急に増え始める入力レベルの応答結果を詳細に調べてみると、建物の梁端部に塑性ヒンジが発生していました。

免震であっても、地震入力レベルを増やしていくと、やがては建物に塑性化が生じます。

そうすると、変形が急激に増え始め、基礎固定よりも大きな変形を生じてしまうことがあるのです。

これが免震の弱点なのです。

実は、この現象は古くから経験的に知られていました^{参考文献4.1）、4.2）}。

【図4.1 免震建物モデル】

fixed:基礎固定、isolated:免震
【図4.2 静的増分解析結果（1階）】	【図4.3 入力地震動レベルと建物1階層間変形の関係】

定常振動による考察

前項でご紹介した特異な応答性状の原因を追究するためのヒントが、Kelly先生の講義にありました。

Kelly先生の講義では、摩擦ダンパーを用いた免震システムの応答性状を調べるために、Den Hartogの非線形定常振動理論^{参考文献4.3））}を適用していました。

定常振動状態というのは、地震応答のような過渡応答と異なり、免震の設計実務で考えることはあまりありません。

しかし、定常振動状態での応答値は、構造物の振動特性を理解する上で非常に重要な指標となります。

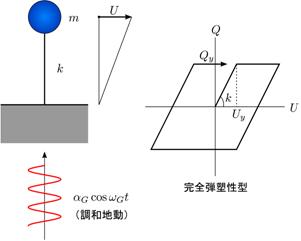
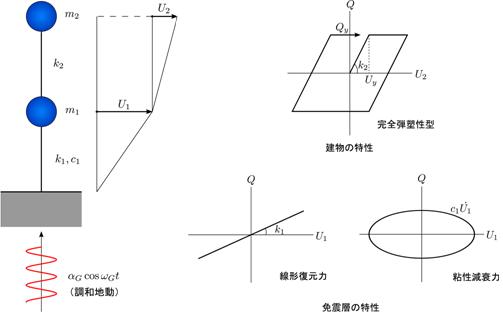
【図4.4】のような1質点振動系に対する調和地動入力を考えます。

地盤が常にsine的に動いている状況です。

ばねは完全弾塑性型とします。

Den Hartogは、定常振動状態における復元力波形をフーリエ級数で近似して、最大変形を求めました。

Den Hartogの方法を使って、【図4.6】のような非減衰完全弾塑性型1質点振動系の定常振動応答の振幅を求めてみます。

振幅Uは、降伏変位U_yで割って塑性率μ(=U/U_y)で表現しますと、(4.1)式のようになります。

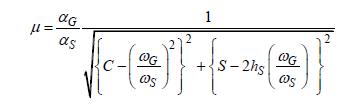
（4.1）

ここに、μは塑性率(=U/U_y)、α_Gは加振加速度振幅、ω_Gは地動の加振振動数、α_Sは降伏点加速度(=kU_y/m)、ω_Sは固有振動数、h_Sは減衰定数です。

係数CとSは(4.2)式から求められます。

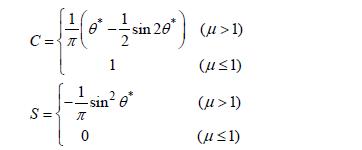
	（4.2）

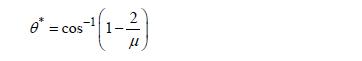
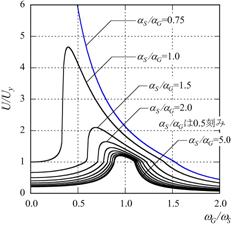
(4.1)式を用いて【図4.5】のように共振曲線を描いてみました。

建物の耐力に相当するばねの降伏点加速度比(α_S/α_G)を変えてみました。

地動加振加速度α_Gを一定とした場合は上の曲線ほど建物の耐力が低くなりますし、建物の降伏点加速度α_Sを一定とした場合には上の曲線ほど大きな地震入力となります。

応答塑性率のピーク振動数が建物の降伏耐力の低下とともに、低振動数側へ移動していくことに着目して下さい。

これは、建物が壊れ始めると剛性が低下し共振振動数がどんどん低下していくという現象を示しています。

さらにグラフの左側に注目して下さい。

グラフの左端に近い方が、地動振動数が低くなる、すなわちより長周期の地動になります。

左端のY軸に達すると、外力は静的に作用することになります。

また、α_S/α_Gが1.0以下は、建物に耐力より大きな荷重が作用することを意味します。

荷重が動的であれば、建物の質量が慣性力となって抵抗できます。

慣性力による抵抗はグラフの右側に近い方が大きくなります。

しかし、グラフの左側のように荷重が静的に作用すれば、建物の耐力以上には抵抗しにくくなります。

青い線で描いたα_S/α_G=0.75の曲線が左上に上がったまま戻ってこないのは、建物が荷重に抵抗できず大きな変形が生じて壊れてしまうという現象が、数学的には発散という形で現れていることを意味します。

【図4.4 完全弾塑性1質点振動系】	【図4.5 共振曲線】

免震で同様の検討を行うには、2質点振動系が必要となります。

そこで、【図4.6】のような2質点振動系の定常振動について考えてみました。

田治見先生が2質点振動系の非線形定常振動については研究を行われていて、その知見については振動学の教科書としても執筆されています^{参考文献4.4））}。

ただし、免震を意識されたものではなく、計算例も限られたものでした。

そこで田治見先生の定式化を参考に、これを免震風にアレンジした定式化を行ってみました。

方程式は1質点系と比べてかなり複雑になりましたので、ここではその説明を割愛します。

詳細な定式化に興味のある方は、拙論^{参考文献4.5））}をご覧になってください。

【図4.6 調和地動下での2質点振動系】

それでは、計算結果について説明します。

似たようなグラフを並べていますが、よく見るとすべて異なっています。

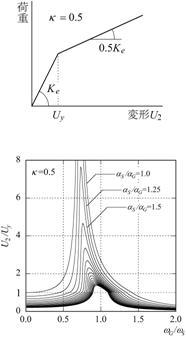
(a) 基礎固定（左から剛性低下率K=0.1,0.2,0.5）
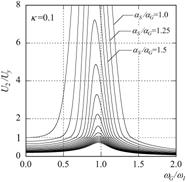
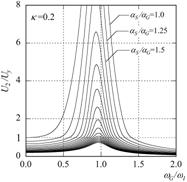
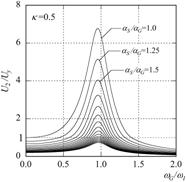
(b) 免震（左から剛性低下率K=0.1,0.2,0.5）
【図4.7 共振曲線の比較】

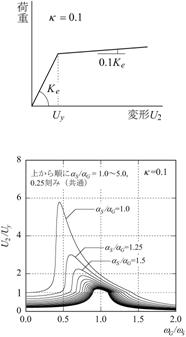
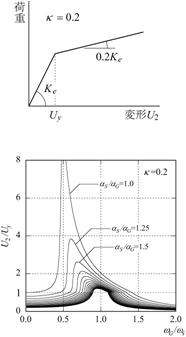
【図4.7】の6つのグラフは、基礎固定と免震に対して、建物部分の降伏後剛性の低下率_K（弾性剛性K_eに対する低下率）を3通り（_K =0.1, 0.2, 0.5）に変えて計算したものです。

各グラフにおいて、上の曲線ほど建物の耐力が低くなる、あるいは大きな地震動となります。

降伏後の剛性低下の変化に対する共振曲線の移り変わりを、3つ並べた左－中－右のグラフで比較して見て下さい。

(a)の基礎固定では左側のグラフの方が右側のそれよりも塑性率が小さくなります。

これは建物が塑性化して程よく履歴減衰が発揮された方が、塑性率が小さくなるということを示しています。

逆に右側のグラフのように、あまり剛性低下しないとエネルギー吸収に乏しくなります。

(a)の基礎固定のグラフは、現行に耐震設計における構造特性係数D_Sのコンセプトを表しています。

靭性に富む構造であれば、エネルギー吸収をより多く期待できるので、必要保有耐力を下げることができるという訳です。

続いて、(b)の免震を見てみましょう。

(a)の基礎固定とは決定的に異なる点が2つあります。

1つ目は、どの曲線のピーク振動数も同じであり、建物耐力の大小（あるいは地震入力の大小）に応じた変化が見られないということです。

2つ目は、右側のグラフの方が左側のそれよりも塑性率が小さくなるということです。

これは、免震では降伏後剛性を低下させない方が、塑性化を抑えられることを意味します。

逆に大きく壊れて剛性低下してしまうと、塑性率も大きくなってしまいます。

つまり、免震では、履歴減衰による応答の低減効果が期待できません。

これは、(a)の基礎固定と全く逆の傾向です。

どうして、基礎固定と免震ではこのような差が生じたのでしょうか。

それは、免震層上部の建物がいつも3～4秒程度の免震周期で揺らされるからです。

建物が塑性化して剛性低下したとしても、免震装置の柔らかい剛性で決まってしまう建物全体の周期にはほとんど影響ありません。

免震の共振曲線のピーク振動数が、建物の塑性率の大小に関わらず変化しない原因はここにあります。

では、建物が塑性化の程度に関わらず、3～4秒程度の免震周期で揺らされたらどうなるでしょうか。

建物にはほとんど静的に近い荷重が作用し続けるということです。

基礎固定の建物が履歴減衰によって応答が低減されるのは、塑性化して周期が伸びたとしても依然として免震周期より短い周期で振動することで、繰り返しエネルギーが吸収され履歴減衰が有効に作用するからです。

一方、免震のように静的荷重を受ける状況下では、建物の変形を抑えるのは剛性しかありません。

ですから、剛性があまり低下しない方が変形を抑制できますし、逆の場合はどんどん変形が進んでしまいます。

免震は、打たれ弱く脆いと言えます。

基礎固定の場合は、塑性化が履歴減衰の増大となり変形を抑制する方向に働きますから、冗長性という観点からは基礎固定の方が一枚上手です。

この現象は、最初にお話した建物の地震応答解析結果の意味するところと合致します。

以上が、過渡応答でも定常応答でも共通して見られる免震の応答特性なのです。

免震の建物は一度壊れるとどんどん変形が進んでしまいますから、免震の建物を塑性化させる設計は好ましくないということになります。

免震設計への警鐘

ここまで免震の弱点ばかり追求してきましたが、それは免震の建物が塑性化した場合の話です。

基礎固定と免震とでは、建物が壊れるまでの余裕に大きな差があります。

現行の耐震基準のように、基礎固定では塑性化を前提とした設計が行われているのに対して、免震ではレベル2と言われる地震動に対しても、建物を弾性状態で維持させることは難しくありません。

注意して頂きたいのは、想定以上に大きな地震入力があった場合です。

あるいは、建物の耐力に全く余裕のない設計をした場合です。

基礎固定では想定以上の地震入力があったとしても劇的な変化はありませんが、免震の場合は変形の急増というように状況が一変します。

おわりに

今回お話した内容については、SIE Inc.^{参考文献4.6）}のエンジニアであるDr. Cameron J. BlackとDr. Ian D. Aikenの3人で論文を発表しました^{参考文献4.5）}。

Black氏の提案により、論文では免震と基礎固定の応答特性を表現する英語として、免震はself-propagatingであり、基礎固定はself-limitingであるという表現を用いました。

私はこれらの単語が、これまで長々を説明してきた現象を最も端的に表現できるものとして、非常に気に入っています。

実は、米国の免震設計基準は以上に述べた免震の特異な非線形応答を考慮したものとなっていて、日本ほど建物の耐力を落とすことはできません。

ただし、この基準に従うと、基礎固定以上に高い耐力を要求されてしまうこともあるようです。

それも少し行き過ぎのような感じがします。

免震の設計法に関しては、日米双方でまだ検討の余地が大いにありそうです。

参考文献

4.1)

田村和夫，菊地優：免震RC造骨組の弾塑性応答特性，日本建築学会大会学術講演梗概集B，pp.651-652，1990年

4.2)

菊地優，田村和夫，和田章：免震構造物の安全性評価に関する一考察，日本建築学会構造系論文集，第470号，pp.65-73，1995年

4.3)

Den Hartog JP. Forced vibrations with Coulomb and viscous frictions. Transactions of the ASCE, 1931; APM-53-9: 107-115.

4.4)

田治見宏：建築振動学，コロナ社，1976年

4.5)

Masaru Kikuchi, Cameron J. Black, Ian D. Aiken, ‘On the response of yielding seismically isolated structures’, Earthquake Engineering and Structural Dynamics, Vol. 37, 659-679, 2008.

4.6)

http://www.siecorp.com/