
|
- 1. 強震動予測に用いられる震源モデル
- 2. 地震本部の強震動予測のための「レシピ」とその課題
- 3. 熊本地震などによる地震本部の「レシピ」の検証
- 4. 内陸地震による強震動と永久変位の予測のための断層モデル設定法
- 5. 海溝付近の巨大地震による強震動と津波の予測のための断層モデル設定法
- 6. 相模トラフと南海トラフの巨大地震による予測強震動
|

壇 一男
(だん かずお
/ Kazuo Dan)
- 1960年
- 福岡県山門郡瀬高町(現在、福岡県みやま市瀬高町)にて出生
- 1982年
- 東京大学 工学部 建築学科 卒業
- 1984年
- 東京大学 大学院 工学系研究科 建築学専攻 修士課程 終了
- 1984年
- 清水建設 株式会社 入社
- 1989年
- 中国国家地震局工程力学研究所にて共同研究 (3月~7月)
- 1991年
- 東京大学より学位授与
- 2020年
- 清水建設 株式会社 定年退職
- 2020年
- 熊本大学赴任 現在に至る
■所属学協会
日本建築学会
日本地震工学会
■受賞歴
- 2000年
- 日本建築学会 奨励賞
- 2007年
- 日本建築学会 学会賞(論文)
熊本大学建築構造・防災研究室
http://hagane.arch.kumamoto-u.ac.jp/#3
構造物の耐震設計では、入力地震動として断層モデルによる予測地震動が用いられる事例が増えてきました。本シリーズでは、強震動予測の歴史的な経緯とともに、その最先端の成果について紹介したいと思います。
1. 強震動予測に用いられる震源モデル
我が国では、強震動を予測する場合、政府の地震調査研究推進本部(2017)1) がとりまとめた強震動予測のための「レシピ」に従って断層モデルを設定して地震動を計算することが多く、多くの実務的な事例が蓄積されています。複雑な断層破壊の特徴をとらえて単純化した震源モデルを特性化震源モデルと呼びますが、「レシピ」では、特性化震源モデルのうちアスペリティモデルが採用されています。ここでいうアスペリティモデルとは、断層面が、強震動を生成するアスペリティと強震動を生成しない背景領域の2つから構成されるモデルです。
世界的に見た場合、アスペリティモデル以外にも複数の震源モデルが、強震動予測に用いられていますので、今回は、地震動の再現に用いられてきた震源モデルの歴史的な流れを整理した上で、強震動の予測に用いられている震源モデルについて紹介したいと思います。
1.1 地震動再現のための震源モデルの発展
(1)点震源モデル
地震記録の蓄積および食い違い理論の発展により、震源メカニズムと地球の構造が明らかにされるにつれ、長周期の実体波や表面波の伝播および地球の自由振動が数学的に表現されるようになりました。はじめに用いられた震源モデルは、点震源モデルで、地震波形の周期と比べると断層面上の食い違いが十分に短い時間のうちに形成されるというモデルでした。点震源モデルを用いて、例えば、Kanamori and Given(1981)2) は、1978年宮城県沖地震($\small M_W 7.4$)で得られた周期200秒前後の観測波形を非常によく再現しました。
(2)線震源モデル
点震源モデルは、主に、ごく長周期の地震波形を対象としたものであり、これに対して、食い違いが形成される時間と同等、もしくはそれより短い周期の地震波形は、この食い違いの時間変化に影響を受けます。
Ben-Menahem(1961)3) は、有限の長さの断層上を一定の速度で破壊が進行する線震源モデルを考え、これにより励起される表面波を計算して、実際の長周期表面波の記録との比較から断層の長さと破壊の伝播速度を見積る方法を提案しました。この方法により、Ben-Menahem and Toksoz(1963)4) は、1952年カムチャッカ地震($\small M_W 9.0$)の断層の長さを700km、破壊伝播速度を3km/sと求めました。
(3)面震源モデル(ハスケルモデル)
Haskell(1964)5) は、【図1】に示すように、断層モデルを、その長さ、幅、すべり量、すべり時間関数の立ち上がり時間、および破壊伝播速度の計5個のパラメータで記述し、無限弾性体内に位置する長方形の断層面上を食い違い破壊が進行するモデル(通称、ハスケルモデル)を考え、このモデルにより励起される弾性波のうち遠方で観測される地震波のエネルギーについて考察しました。
その後、Aki(1968)6) は、ハスケルモデルと類似のモデルを用いて、1966年米国Parkfield地震($\small M_W 6.1$)の際に断層近傍の観測点で得られた加速度記録を積分した変位波形と、断層モデルによって計算される理論波形を比較し、両者の主要動が概ね一致することを示しました。
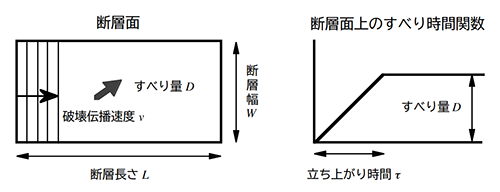
【図1】ハスケスモデル
(4)多重震源モデル
遠地におけるごく長周期あるいは長周期の表面波の解析を行うことによって、断層の大まかな破壊の様子が推定できるようになりましたが、同じく遠地におけるやや長周期の実体波の解析により、震源をより詳しく見ようとする研究も盛んに行われています。
Kanamori and Stewart(1978)7) は、【図2】に示すように(Kanamori, 1979)8)、1976年グアテマラ地震($\small M_W 7.5$)について、9個のサブイベントの位置、発震時刻、およびその地震モーメント(規模)を同定しました。このような震源モデルを「多重震源モデル」とよんでいます。
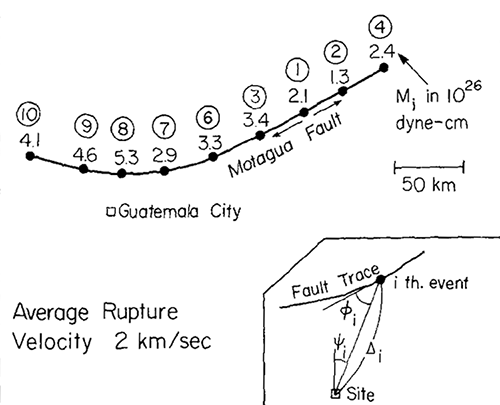
【図2】1976年グアテマラ地震($\small M_W 7.5$)の多重震源モデル
(Kanamori, 1979)8)
(5)非一様すべりモデル
多重震源モデルは、震源をいくつかの点震源の和として表現したモデルであり、各点震源の位置と大きさを求めることがテーマでありますが、これに対し、あらかじめ断層面を設定して、断層面を構成する要素断層におけるすべり時間関数を求める研究も盛んに行われています。このような方法で得られる震源モデルは、「非一様すべり破壊モデル」と呼ばれています。
断層の非一様すべり破壊モデルが求められるようになったのは、1979年米国Imperial Valley地震($\small M_W 6.5$)の断層近傍で、豊富な強震加速度記録が得られてからです。耐震設計で用いられてきたエルセントロの記録は、1940年に起こったImperial Valley地震で観測されたもので、地震の再来を予測して、断層付近に観測網が整備されていました。
1.2 地震動予測のための各種震源モデル
上述した研究成果をうけて、現在、想定地震による強震動を予測するための断層モデルとしては、大きく2つの方法が考えられています。ひとつは、過去の地震の非一様すべり破壊モデルをそのまま、もしくは定数倍したモデルを用いる方法です。もうひとつは、断層の非一様すべり破壊モデルの統計的性質を抽出して、それをもとに特性化した断層モデルを設定する方法です。
特性化震源モデルには、Kikuchi and Fukao(1987)9) などが提案している階層構造モデルおよびSomerville・他(1993)10) などが提案しているアスペリティモデルと波数スペクトルモデルがあります。
ここでは、過去の地震の非一様すべり破壊モデルをそのまま用いる方法、過去の地震の非一様すべり破壊モデルを定数倍して用いる方法、アスペリティモデル、および波数スペクトルモデルを紹介します。
(1)過去の地震の非一様すべり破壊モデル
過去の地震の非一様すべり破壊モデルをそのまま強震動予測に用いるのは、一見、予測問題とはいえないと思われますが、過去に起った地震が再来したときのことを想定して、これまでに強震動が得られていない場所の強震動を予測するものです。
【図3】に、Wald and Somerville(1995)11) による1923年関東地震($\small M_W 7.9$)の非一様すべり破壊モデルを示します。このモデルは、震源付近の測地学的なデータと世界中の遠地における地震記録から同定されたものです。壇・他(2000)12) は、この非一様すべり破壊モデルと関東地方の地下構造モデルとを用いて、【図4】に示すように、広域の震度分布を再現しました。また、このときに計算された強震動は、超高層建物や免震建物の耐震設計に用いられています。
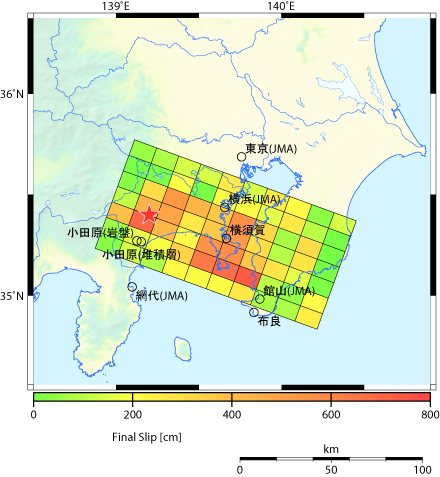
【図3】1923年関東地震($\small M_W 7.9$)の非一様すべり破壊モデル
(Wald and Somerville, 199511) より作成)
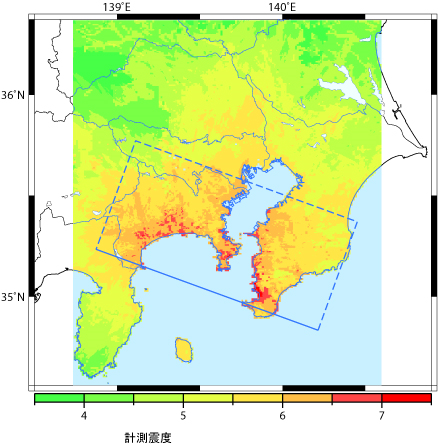
【図4】1923年関東地震($\small M_W 7.9$)の広域の震度分布の再現
(壇・他, 2000)12)
(2)過去の地震の非一様すべり破壊モデルを定数倍したモデル
Heaton et al.(1995)13) は、1992年米国Landers地震($\small M_W 7.2$)の断層の非一様すべり破壊モデルを定数倍したものをロサンゼルス市直下で想定される地震($\small M_W 7.0$)の断層モデルとして用いています。また、この断層モデルを用いて地震動を計算したところ、大振幅の変位波形と速度波形が得られ、それを20階建の鉄骨造建物と3階建の免震建物に入力した結果、鉄骨造建物は倒壊の可能性があること、免震建物はその機能性を確保するには例外的な方策を講じる必要があると述べています。
(3)特性化震源モデルのうちアスペリティモデル
アスペリティは、英語のasperityであり、「荒々しさ」あるいは「でこぼこ」という意味です。Kanamori(1981)14) は、地震の発生域では、高強度の領域(アスペリティ)とそのまわりの低強度の領域(背景領域)があると考えるアスペリティモデルを示して、メキシコ、日本、南米などの長さが数千kmにおよぶ地震の発生域で起きた多くの地震の発生様式を説明しました。Das and Kostrov(1986)15) は、地震群に適用されたKanamori(1981)14) のアスペリティモデルを、ひとつの地震に対して適用しました。
その後、1995年に起った兵庫県南部地震では、震度7の震災の帯ができ、その原因が周期1秒の強震動パルスであったこと(川瀬, 1998)16)、この強震動パルスは断層面全体ではなく、アスペリティとよばれる狭い領域から放出され、破壊が進行する方向に地震波が重なったことが解明されました。【図5】に、震災の帯を引き起こした強震動パルスとその原因となったアスペリティ(松島・川瀬, 2009)17) を示します。
冒頭で述べたように、地震調査研究推進本部(2017)1) による強震動予測のための「レシピ」では、このアスペリティモデルを採用しています。
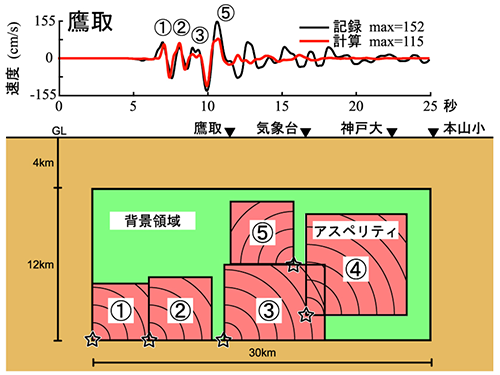
【図5】1995年兵庫県南部地震の強震動パルスとその原因となったアスペリティ
(松島・川瀬, 2009より作成)17)
(4)特性化震源モデルのうち波数スペクトルモデル
Somerville・他(1993)10) は、北米アメリカの11の地震と日本の7つの地震について得られている断層面上のすべり量の空間変動を、断層の長さと幅の2つの方向に関して別々に相関を調べて定量化し、すべり量の波数スペクトルモデルを提案しました。
【図6】に、Saikia and Somerville(1997)18) が、波数スペクトルモデルを用いて生成した$\small M_W 7.0$の地震の非一様すべり分布の例を示します。【図6】では、4つの例しか引用していませんが、乱数を用いているため、波数スペクトルモデルを満たす非一様すべり破壊モデルはいくつでも生成することができます。アメリカにおける強震動予測には、この波数スペクトルモデルがよく用いられています。
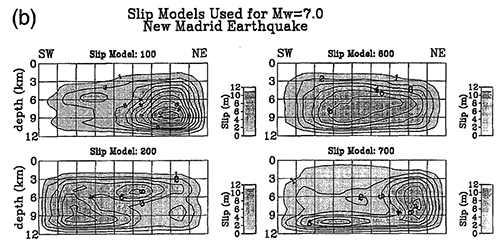
【図6】波数スペクトルモデルを用いて生成した$\small M_W 7.0$の地震の非一様すべり分布の例
(Saikia and Somerville, 1997)18)
参考文献
- 1)
- 地震調査研究推進本部(2017):震源断層を特定した地震の強震動予測手法(「レシピ」), https://www.jishin.go.jp/evaluation/strong_motion/
- 2)
- Kanamori and Given(1981):Use of long-period surface waves for rapid determination of earthquake-source parameters, Physics of the Earth and Planetary Interiors, Vol. 27, No. 1, pp. 8-31.
- 3)
- Ben-Menahem(1961):Radiation of seismic surface-waves from finite moving sources, Bulletin of the Seismological Society of America, Vol. 51, No. 3, pp. 401-435.
- 4)
- Ben-Menahem and Toksoz(1963):Source mechanism from spectra of long-period seismic surface waves, 2. The Kamchatka earthquake of November 4, 1952, Journal of Geophysical Research, Vol. 68, No. 18, pp. 5207-5222.
- 5)
- Haskell(1964):Total energy and energy spectral density of elastic wave radiation from propagating faults, Bulletin of the Seismological Society of America, Vol. 54, No. 6, pp. 1811-1841.
- 6)
- Aki(1968):Seismic displacements near a fault, Journal of Geophysical Research, Vol. 73, No. 16, pp. 5359-5376.
- 7)
- Kanamori and Stewart(1978):Seismological aspects of the Guatemala earthquake of February 4, 1976, Journal of Geophysical Research, Vol. 83, No. B7, pp. 3427-3434.
- 8)
- Kanamori(1979):A semi-empirical approach to prediction of long-period ground motions from great earthquakes, Bulletin of the Seismological Society of America, Vol. 69, No. 6, pp. 1645-1670.
- 9)
- Kikuchi and Fukao(1987):Inversion of long-period P-waves from great earthquakes along subduction zones, Tectonophysics, Vol. 144, Nos. 1-3, pp. 231-247.
- 10)
- Somerville・他(1993):地震断層のすべり変位量の空間分布の検討, 第22回地震工学研究発表会講演概要, pp. 291-294.
- 11)
- Wald and Somerville(1995):Variable-slip rupture model of the great 1923 Kanto, Japan, earthquake, Bulletin of the Seismological Society of America, Vol. 85, No. 1, pp. 159-177.
- 12)
- 壇・他(2000):統計的グリーン関数法による1923年関東地震(MJMA7.9)の広域強震動評価, 日本建築学会構造系論文集, No. 530, pp. 53-62.
- 13)
- Heaton et al.(1995):Response of high-rise and base-isolated buildings to a hypothetical MW 7.0 blind thrust earthquake, Science, Vol. 267, pp. 206-211.
- 14)
- Kanamori(1981):The nature of seismicity patterns before large earthquakes, Earthquake Prediction-An International Review, American Geophysical Union, Maurice Ewing Volume 4, pp. 1-19.
- 15)
- Das and Kostrov(1986):Fracture of a single asperity on a finite fault: A model for weak earthquakes?, Earthquake Engineering, Vol. 2, pp. 2385-2396.
- 16)
- 川瀬(1998):強震動特性と地下構造, 第26回地盤震動シンポジウム, pp. 9-20.
- 17)
- 松島・川瀬(2009):1995年兵庫県南部地震での神戸市域における強震動と木造建物被害の再評価, 構造工学論文集, B(55B), pp. 537-543.
- 18)
- Saikia and Somerville(1997):Simulated hard-rock motions in Saint Louis, Missouri, from large New Madrid earthquakes($\small M_w \geqq 6.5$), Bulletin of the Seismological Society of America, Vol. 87, No. 1, pp. 123-139.