第2回 免震の要、積層ゴム

はじめに

今回は、積層ゴムを扱います。

積層ゴムは、免震の要（かなめ）です。積層ゴムに関する一般的な知識については、例えば日本免震構造協会から刊行されている「免震積層ゴム入門」^{参考文献2.1）}に譲ることとして、ここでは筆者が積層ゴムと格闘した10年間についてお話します。

便利だけど扱いづらかった積層ゴム

免震に関わってきた20年間のうち、約半分の期間は積層ゴムの素性を理解することに費やしました。

特に、支承減衰一体型の積層ゴムである高減衰積層ゴムや鉛プラグ入り積層ゴムの素性を明らかにして、これらの積層ゴムを使う設計手法の確立はライフワークとなりました。

支承減衰一体型の積層ゴムがダンパーを不要にできる理由は、履歴減衰を有しているからです。

免震の企画・設計・施工までを一貫して担当した経験から思うことは、やはり一体型の積層ゴムは便利ということです。

ただし、この判断には、力学的特性を適切に評価できることが前提となります。

履歴減衰は、載荷時と除荷時で違う経路を通ることで生じる現象です。

この現象を2折れ線で近似することがよく行われます。

いわゆる、バイリニアモデルの適用です。

しかし、通常のバイリニアモデルでは、変形に応じて履歴ループ形状が変化するという支承減衰一体型の積層ゴムに見られる現象を捉えきれないために、バイリニアモデルのパラメータを変形に応じて更新するという方法（修正バイリニアモデル）が用いられています。

初回でお話したカリフォルニア大学での免震建物の振動台加振試験では、高減衰積層ゴムにせん断ひずみで300%を超える変形が生じたために、修正バイリニアモデルでも試験結果を再現できませんでした。

ゴムはせん断ひずみが300％を超える変形領域に達すると硬化する性質があります。

カリフォルニア大学との共同研究を総括するには、振動台加振試験結果を解析的に再現しなければならないという状況にあったために、積層ゴムの復元力モデルの開発に着手しました。

修正バイリニアモデルに代わるもの

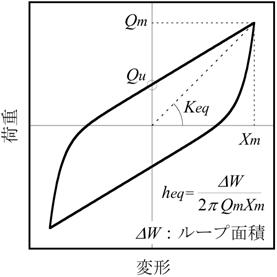
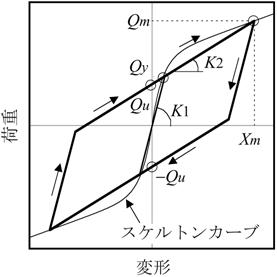
高減衰積層ゴムのモデル化で多用されているのは、【図2.1】に示す修正バイリニアモデルです。

高減衰積層ゴムの力学的特性は、等価せん断弾性率G_eq、等価粘性減衰定数h_eq、荷重切片比uという3つの復元力指標で評価されます。

いずれの指標もせん断ひずみの関数として表現されます。

バイリニアの形を決める初期剛性K₁、降伏後剛性K₂、降伏荷重Q_yは、それらの3つの指標を満足するように方程式を立てることで、（2.1）～（2.3）式から決定できます。

	（2.1）
	（2.2）
	（2.3）

ここに、K_eqは積層ゴムの等価剛性であり（【図2.1(a)】参照）、ゴム層の総厚H_r、ゴムの断面積A_r、ゴムの等価せん断弾性率G_eqを用いて、（2.4）式によって求められます。

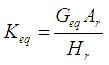
(2.4)

(a) パラメータの定義	(b) 履歴則
【図2.1 修正バイリニアモデル】

修正バイリニアモデルは、通常の設計で想定する変形（せん断ひずみ250%程度）であれば問題はないのですが、それ以上の変形となるとハードニングやそれに続く特異な履歴ループ形状を表現できなくなります。

そこで、藤田隆史先生らが提案されていた修正Rateモデルというモデルを調べてみました^{参考文献2.2）}。

Rateというのは、速度を意味していて、復元力が変位と速度の項を含む微分方程式の形で表現されています。

微分方程式であれば、境界条件を設定して解くことができます。

解いてみると、自然対数eを含む滑らかな曲線であることがわかりました。

Rateモデルはe関数の柔軟性と曲線の滑らかさが魅力的であり、紡錘形の履歴ループに対しては良い近似を与えました。

しかし、大変形時に現れる特異な履歴ループ形状を表現することが、Rateモデルでもできませんでした。

そこで、Rateモデルに修正を加えて、途中まではオリジナルのRateモデルとし、ハードニングが生じると修正項（（2.7）式中の係数bの項）が有効になるようなスイッチを入れました。

（2.5）～（2.7）式が最終形です。

	（2.5）
	（2.6）
	（2.7）

ここに、Q_mはスケルトンカーブからの除荷時の荷重であり、xは無次元化変位 (x=X/Xm)です。（2.6）式のnはハードニングを規定するパラメータです。

（2.7）式におけるa、bは、実験より得られた履歴ループ面積と解析モデルによるそれを等価にするという条件により、（2.8）、（2.9）式から求めます。

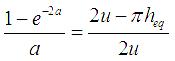
	（2.8）
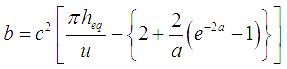
	（2.9）

ここに、cは履歴ループの形状を操作するパラメータであり、あらかじめ決定しておきます。

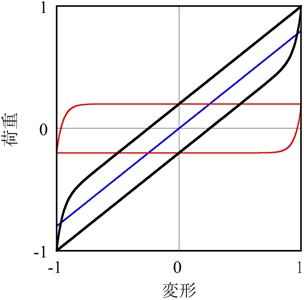
【図2.2】に（2.5）～（2.7）式から得られる履歴ループ形状を無次元化して示しています。

このモデルでは、まず初めに復元力Qを非線形弾性成分Q₁と履歴減衰成分Q₂に分離します。

非線形弾性成分Q₁は剛性を操作します。

履歴減衰成分Q₂は、載荷と除荷で違う経路を規定して履歴ループの面積を調整します。

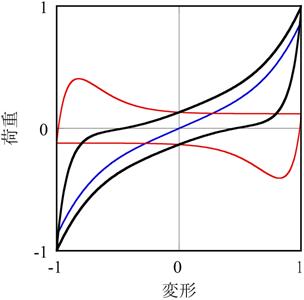
【図2.2】では、パラメータの組み合わせを2通り示しています。

【図2.2(a)】はb=0とした場合であり、従来のRateモデルと一致します。

これらのパラメータはせん断ひずみの関数ですので、ひずみの増大に応じて【図2.2(a)】から【図2.2(b)】へは滑らかに移行できます。

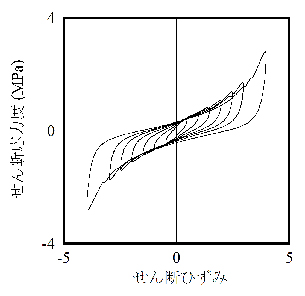
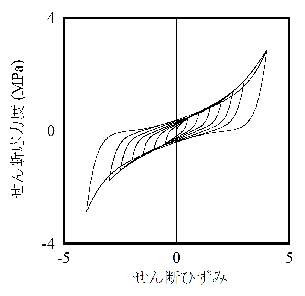
【図2.3】は高減衰積層ゴムの加力試験結果を再現してみた結果です。

両者は非常に良く合っています。

(a) 低ひずみレベル	(b) 高ひずみレベル
【図2.2 提案モデルの無次元化履歴ループ】

(a) 試験結果	(b) 解析結果
【図2.3 高減衰積層ゴムのシミュレーション解析】 （試験データ提供：東洋ゴム工業）

復元力モデルの拡張

さて、高減衰積層ゴムの復元力モデルは完成したものの、鉛プラグ入り積層ゴムについては、全くの手付かずの状態でした。

両者は支承減衰一体型の積層ゴムであり、使い勝手の点で共通点が多いことから、鉛プラグ入り積層ゴムに対しても適用できるようなモデルの拡張に着手しました。

鉛プラグ入り積層ゴムの履歴ループは鉛プラグの降伏荷重に対応したバイリニア型の形状を示します。

しかし、完全なバイリニア型とはならず、履歴ループ形状は経験せん断ひずみによって変化しますので、高減衰積層ゴムと同様に修正バイリニアモデルが用いられています。

ただし、パラメータ評価式は、両者で大いに異なります。

鉛プラグ入り積層ゴムは、構成する天然ゴム部および鉛プラグの物性値と形状（厚さ、断面積等）から、バイリニアモデルの初期剛性、降伏後剛性、荷重切片を直接的に評価する設計式が存在します^{参考文献2.3）}。

その設計式を取り込んで復元力モデルを拡張することに関して、あるアイディアが浮かびました。

それは、まず初めに設計式を用いてバイリニアモデルを作り、その履歴ループ面積から等価粘性減衰定数を計算すればよいのです。

（2.10）式は、鉛プラグ入り積層ゴムの修正バイリニアモデルから計算される等価粘性減衰定数です。

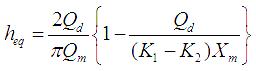
（2.10）

ここに、K₁、K₂は鉛プラグ入り積層ゴムの修正バイリニアモデルにおける1次剛性と2次剛性です。

Q_dは荷重切片、X_mとQ_mは変形と荷重の最大値です。K₁、K₂、Q_uはいずれも設計式から評価できます。

（2.10）式のh_eqを（2.8）式のh_eqと置き換えれば、すべてのパラメータを決定することができます^{参考文献2.4）}。

当初、鉛プラグ入り積層ゴムの復元力モデルは、設計式の適用限界せん断ひずみである250%以下で運用されていました。

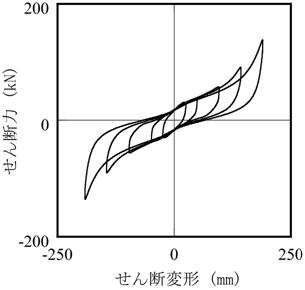
その後、大変形領域での試験データが蓄積されるようになり、それらを分析することによってせん断ひずみ400%まで拡張しました^{参考文献2.5）}。

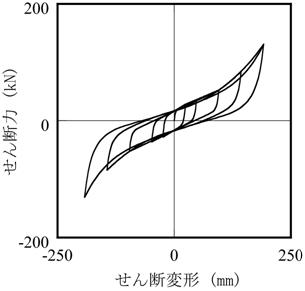
(a) 試験結果	(b) 解析結果
【図2.4 鉛プラグ入り積層ゴムのシミュレーション解析】

統一的復元力モデルの構築

拡張復元力モデルは、徐々に実際の免震設計に使われるようになりました。

そこに、高減衰積層ゴム、鉛プラグ入り積層ゴム、鋼棒ダンパー（ループダンパー）を3種類の装置を組み合わせた免震レトロフィットの話が舞い込んで来ました^{参考文献2.6）}。

これら3種類の免震装置の力学的特性を正確に再現することがコストダウンにとって重要であると聞き、さっそく鋼棒ダンパーへの拡張を試みました。

鋼棒ダンパーの実験データを、高減衰積層ゴムのときと同じ3種類の復元力指標によって分析し、先に提案した復元力モデルを適用してみたところ、荷重変形関係を非常に精度良く再現できることがわかりました。

復元力指標はダンパーのタイプ・サイズごとに用意する必要があるのですが、種類はそれ程多くないため手間にはなりません。

その後、同じく鋼材系のダンパーであるU型ダンパーへの適用も成功しました。

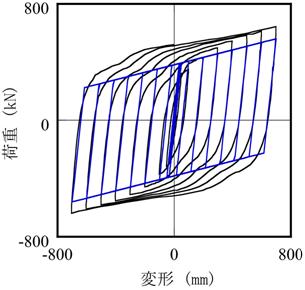
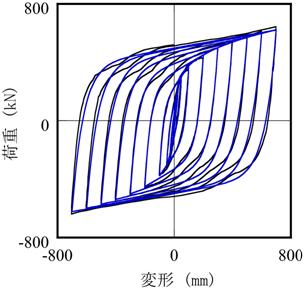
【図2.5】は鋼棒ダンパーへの適用例です。

比較のために、通常用いられているバイリニアモデルも示しています。

拡張復元力モデルは、バイリニアモデルよりも正確に鋼棒ダンパーの履歴減衰性能を評価していることがわかります。

以上のように、タイプの異なる免震装置であっても、復元力特性の分析方法を共通化すると、荷重変形関係を統一的に表現できることがわかりました^{参考文献2.7）}。

現在は、免震装置の力学特性データの提供体制も確立され、新たに開発される免震装置はタイムリーに解析システムに反映され、設計で使用できるようになりました。

(a) バイリニアモデル	(b) 提案モデル
【図2.5 鋼棒ダンパーへの適用】

おわりに

第2回は、積層ゴムと格闘した約10年を振り返ってみました。

2005年には、今回お話した復元力モデルの技術的有用性が認められ、日本免震構造協会賞（技術賞）を頂きました。

また、このモデルに「菊地モデル」という名称も頂きました。

昨年、菊地モデルを用いて設計された免震建物の棟数を数えてみたら、100棟を超えていたことがわかりました。

ずいぶん使われているなぁと思いつつも、まだ日本の全免震建築棟数2000棟の5%でしかありません。

昨年になって、ようやく海外で1件使われました^{参考文献2.8）}。

これからも、性能向上と改良に努めます。

参考文献

2.1)

日本免震構造協会：免震積層ゴム入門，オーム社，1997年

2.2)

藤田隆史，鈴木重信，藤田聡：建物免震用の高減衰積層ゴムに関する研究（第1報，履歴復元力の基本特性と解析モデル），日本機械学会論文集（C編），56巻，523号，pp.658-665，1990年

2.3)

オイレス工業：LRB技術資料，2000年

2.4)

菊地優，北村佳久，太田雅己：鉛プラグ入り積層ゴムの復元力特性に関する一考察（その1，その2），日本建築学会大会学術講演梗概集B，pp.583-586，1999年

2.5)

小槻淳，山本祥江，菊地優，越川武晃，上田正生：鉛プラグ入り積層ゴムの大変形復元力モデルに関する研究，構造工学論文集，Vol.53B，pp.9-16，2007年

2.6)

Nishimura K., Yagi, T., and Nakao Y., (2002), “Seismic base-isolation retrofit of Central Public Hall in Osaka City”, Structural Engineers World Congress 2000, Japan, Paper No. T8-3-b4

2.7)

菊地優，北村佳久，井上圭一，上田正生：履歴減衰型免震部材の復元力モデルに関する研究，日本建築学会構造系論文集，第565号，pp.63-71，2003年

2.8)

John Sherstobitoff, Mahmoud Rezai, Ian Aiken and Li Yan. Seismic Upgrade of an Intake Tower using Underwater Base Isolation, Preliminary Design; Vancouver Island, Canada, Proceedings of the 14th World Conference on Earthquake Engineering, Beijing, China, Paper ID: 05-06-0155, 2008.