第3回:やさしい免震層の設計
はじめに
免震構造の設計は簡単であるといったら怒られるだろうか。免震建物の上部構造は弾性設計であり、想定される地震力に耐えることができる強度があればよい。免震構造の性能は免震層をどうつくるかにかかっている。免震層にはアイソレータとダンパーが配置される。それらをどう組み合わせるか、変形能力をどれくらい確保するかできるか、などを考える必要がある。アイソレータやダンパーなどに馴染みがないと取り扱いが難しいかと思われるが、ここでは、できるだけやさしくアイソレータやダンパーの設計について解説したい。
免震構造の限界状態
免震層には、積層ゴムやダンパーなどの免震部材が設置される。当然ながら免震部材の設計と免震層周りの設計とは関連がある。通常の構造設計では、構造部材に作用する応力に着目されるが、免震層あるいは免震部材の設計では応力(度)よりも変形量(最大変形、累積変形)が特に重要となる。
免震部材、特にアイソレータ(積層ゴム)の変形能力はどれくらいか、水平剛性をどこまで柔らかくできるか、建物と敷地の関係などにより免震層の可動範囲(許容変形量、クリアランス)をどの程度確保できるのか、などが免震建物の性能を確保する上で重要となる。設計された免震建物の限界状態を想定しておくことは重要である。免震建物に想定外の地震動が入力した場合、免震建物はどういう状態になるのか、逆に言えば、建物のどこを壊すのか。考えられる状態としては、
・アイソレータが破断する
・敷地周辺の擁壁に衝突する
・上部構造が塑性化する
・基礎構造が塑性化する
などが考えられる。アイソレータの破断あるいは擁壁衝突に至るまでの入力レベルを把握することで、免震建物の安全余裕度を評価できる。ただし、衝突時には上部構造に大きな加速度が発生することになる。上部構造や基礎構造の塑性化を先行させることは免震構造の目的から言って最後の選択肢とすべきである。
設計変位$\delta_{dsgn}$と免震クリアランス
免震構造の設計では免震層設計変位と積層ゴムの設計(変形能力)は密接な関係にある。免震層の最大変形量$\small \delta_{max}$は包絡解析法や地震応答解析から求められ、これをもとに免震層の設計変位$\small \delta_{dsgn}$がねじれ応答や2方向入力による影響などを加味して設定されることになる。
【図1】に天然ゴム系積層ゴムの破断試験の結果を示す。ゴムのせん断弾性率は0.45MPa程度である。試験時の面圧が3倍変化しても、復元力特性に変化は見られない。こうした特性を発揮できる積層ゴムのゴム物性と形状を選択することが重要である。積層ゴムの変形性能を表すために「せん断変形率(せん断ひずみ)」が使われる。これは、せん断変形を積層ゴムの全ゴム層厚で除した値である。すなわち、せん断変形率100%は全ゴム層厚と同じせん断変形が生じていることを示している。天然ゴム系積層ゴムのせん断変形時の挙動は、せん断変形率$\small \gamma$=250%まではほぼ線形であり、これ以降ハードニング現象により剛性が徐々に大きくなる。最終的にはせん断変形率400%程度で破断に至る。従って、設計変位としては積層ゴムのせん断変形率で250%程度以下を目標とする事になる。この変形量であれば破断に至るまでには約1.5倍以上の余裕度がある。ハードニングは免震層の変位を抑制するには効果的であるが、免震層のベースシア係数を上昇させることになり、上部構造の応答加速度の観点からは不利である。
水平クリアランスは、敷地の余裕やアイソレータの変形能力、設備配管などの可動距離などとの関連で決定される。免震層の可動範囲は水平クリアランスにより決定されることになり、水平クリアランスをどの様に設定するかは非常に重要である。水平クリアランス$\small \delta_{Hgap}$は設計変位$\small \delta_{dsgn}$より当然大きく設定することになる。ただし、どの程度大きく設定するかは、判断の分かれるところである。もし、水平クリアランスを超えるような応答となる場合には、建物は衝突する可能性があり、逆に積層ゴムの破断変位より大きな水平クリアランスを設定しておけば、積層ゴムの破断が起こることになる。いずれにしても想定している地震動と建物の性能に依存する。逆に、敷地の余裕の制限から設計変位が規定されることもあろう。この場合にも許される変位量の中で発揮できる免震性能を包絡解析法などで確認し、建物の性能を設定していくことが重要である。
鉛直クリアランス$\small \delta_{Vgap}$は、積層ゴムの圧縮変形+せん断変形時の鉛直沈み込み量+クリープ変形を考慮して決定する必要がある。
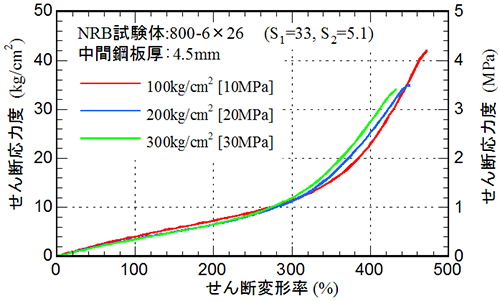
【図1】天然ゴム系積層ゴムの圧縮せん断特性
設計面圧$\sigma_{dsgn}$
積層ゴムの設計軸力を考える場合、常時荷重と地震時転倒モーメントなどによる付加軸力を考慮しなければならない。現在では、天然ゴム系積層ゴムの限界耐力に関する実験研究や高い圧縮面圧のもとでのせん断変形試験を通して、積層ゴムの形状とゴム材質を適切に選択すれば、より高い圧縮応力度に対しても十分な荷重支持能力と変形性能を確保できることが明らかにされてきており、長期面圧として15MPa程度での使用が可能となってきている。
水平剛性の面圧依存性は十分な精度で次式により近似できる。ただし、積層ゴムの面圧依存性については実験などで十分に検証を行うことが重要である。
$$\frac{K_H}{K_{H0}}=1-\left( \frac{\sigma}{\sigma_{cr}} \right)^2 \tag{1}$$
ここで、$\small K_{H0}$:面圧が0の時の水平剛性、$\small \sigma_{cr}$:座屈応力度
面圧0の時に対して水平剛性の低下を10%以内とするためには、積層ゴムの面圧は$\small \sigma_{cr}/3$程度以下とすることが必要である。また、地震時には積層ゴムに転倒モーメントや上下動などによる付加軸力が作用する。積層ゴムには軸力変動による最大面圧下でも安定した変形能力を発揮することが求められる。このためには、積層ゴムの最大面圧に制限を設ける必要があろう。この制限は積層ゴムに求められる水平変形能力と大きな関連を持っているため一概には決められないが、$\small \sigma_{cr}/2$程度が一つの目安になるものと考える。
積層ゴムの座屈応力度はおおむね次式で求められる。なお、座屈応力度に関する詳細は、「免震構造設計指針」(日本建築学会)を参照してほしい。
$$\sigma_{cr}\cong G \cdot S_1 \cdot S_2 \tag{2}$$
ここで、$\small G$:ゴムのせん断弾性率、$\small S_1$:1次形状係数、$\small S_2$:2次形状係数
積層ゴムのせん断変形時の耐荷機構として、単純に有効支持部分だけで圧縮荷重を支持していると仮定すれば、圧縮荷重を有効支持部分の面積$\small A_e$で除した応力度が座屈応力度に達するときが、積層ゴムの安定限界変形であると考えることができる。この様な仮定に基づけば、水平変形量$\small \delta_{cr}$と面圧$\small \sigma$の関係が近似的に次式のように求められる。積層ゴムに作用する軸力の大きさに応じて、限界変形も変化することには留意する必要がある。
$$\frac{\delta_{cr}}{D}=\frac{\gamma_{cr}}{S_2}=1-\frac{\sigma}{\sigma_{cr}} \tag{3}$$
ここで、$\small D$:積層ゴムの直径、$\small \gamma_{cr}$:限界せん断ひずみ
免震層の設計
免震建物では、アイソレータやダンパーの特性を選択することで、地震時の応答性状を決定することが可能である。これは事前に建物の性能を決定・評価できることを示している。従って、免震建物にどのような性能を与えたいかを設計者が決定し、それを実現するように上部構造やダンパーとの関連性を考慮して、積層ゴムの配置、サイズ、個数や面圧などを決定していけばよいことになる。
使用する積層ゴムのサイズや形状は、積層ゴムの性能評価上、品質管理上できるだけ統一した方が良い。ただし、実際には積層ゴムの軸荷重は一様ではないため免震性能を向上させるためには柔らかいゴム材質を持つ積層ゴムや成の高い(2次形状係数の小さい)積層ゴムを使用することもある。この場合、個々の積層ゴムの持つ性能には当然差異があり、これらの特性を十分把握した上で設計することが必要である。
この様な点に配慮すれば、積層ゴムの設計は、大略次の様な手順で行うことができる。
①免震周期$\small T_f$と設計変位$\small \delta_{dsgn}$の設定
建物の用途、地盤種別や応答などを基に、想定する地震入力や免震性能(免震層のベースシア係数や最大変形量)を設定する。これらの性能を満足する設計変位$\small \delta_{dsgn}$や免震周期$\small T_f$を包絡解析法などに基づいて設定する。
②積層ゴムの2次形状係数$\small S_2$とせん断弾性率$\small G$の設定
積層ゴムの形状や材質を設定する。柱軸力の大きさにより形状や材質を変化させる場合には、代表的な$\small S_2$と$\small G$を設定しておく。
2次形状係数$\small S_2$は積層ゴムの座屈性能に関連している。2次形状係数が5程度であれば、軸力変動による水平剛性の変動が小さく、座屈も起こりにくい。
ゴム材料のせん断弾性率$\small G$は積層ゴムの水平剛性や座屈応力度に関連しており、積層ゴムの特性を支配する重要な材料定数である。
③積層ゴム最小径$\small D_{min}$の設定
天然ゴム系積層ゴムの復元力特性より、せん断変形率$\small \gamma$=250%を線形範囲と考え、$\small \frac{D}{\delta_{dsgn}}=\frac{S_2}{\gamma}$の関係より、2次形状係数$\small S_2=5$では$\small D_{min} \geq 2\delta_{dsgn}$、$\small S_2=7$では$\small D_{min} \geq 3\delta_{dsgn}$とする。ただし、2次形状係数が5より小さな積層ゴムを使用する場合でも設計変位が直径の1/2以下程度となるように積層ゴムのサイズを決定する様にする。
④建物平面計画の検討
平面計画が既に決まっている場合には、次のステップ⑤へ。
①で設定した免震周期を達成するために必要な建物全体としての平均面圧$\small \sigma_{ave}$は次式により計算できる。形状や材質の異なる積層ゴムを用いる場合には、平均的な値を用いる。
$$\sigma_{ave}=\left( \frac{T_f}{2 \pi}\right)^2 \frac{GS_{2}g}{D_{min}}=24.8 \frac{T^{2}_{f}GS_2}{D_{min}} \tag{4.1}$$
ここで得られた面圧が座屈応力度の1/3以下程度であることを確認する($\sigma_{ave}\leq\sigma_{cr}/3$)。大きく越えている場合には、設計条件の再検討を行う。(4.1)式より、平均柱軸力$P_{ave}$が次のように求められる。
$$P_{ave}=\frac{g}{16\pi}T^{2}_{f}GS_2D_{min}=19.5T^{2}_{f}GS_2D_{min} \tag{4.2}$$
(4.2)式の平均柱軸力を満足するように、建築物の平面計画、構造計画を検討する。満足できない場合は設計条件の見直しを行うことが必要となる。
⑤個々の積層ゴムの設計
(4.1)式により算出される平均面圧$\small \sigma_{ave}$となるように積層ゴムの直径$\small D$を設定する。積層ゴムの直径は③で設定した最小径$\small D_{min}$以上とする。設定した直径より、積層ゴムの面圧$\small \sigma$を算出し、面圧の大きさを把握する。面圧の大きさを考慮しながら、2次形状係数$\small S_2$とせん断弾性率$\small G$を個別に決定する。
⑥積層ゴムの水平剛性の総和$\small \sum K_H$を算出
⑤で決定された積層ゴムの水平剛性を算出し、免震層全体の水平剛性$\small \sum K_H$を求める。水平剛性は、中心孔径が小さい場合には次式で略算できる。
$$K_{H0}=\frac{\pi}{4}DS_2G \tag{5}$$
中心孔が大きい場合には、座屈荷重を低下させる要因となるので、中心孔はできるだけ小さい方がよい。
⑦免震周期の比較
⑥で求められた水平剛性$\small \sum K_H$より周期$\small T_{f0}$を次式により計算する。
$$T_{f0}=2\pi\sqrt{\frac{W}{\sum K_H\cdot g}} \tag{6}$$
ここで、$\small W$:建物全重量、$\small g$:重力加速度
①で設定した免震周期$\small T_f$と$\small T_{f0}$の比較を行い、両者がほぼ一致する場合には⑧へ、異なる場合には⑤へ戻り積層ゴムの再設定を行う。
⑧積層ゴムの仕様の決定
積層ゴムの1次形状係数$\small S_1$は、積層ゴムのゴム厚$\small t_R$とゴム層数$\small n$に関係している。全ゴム層厚は2次形状係数より決定されるため、1次形状係数を満足するようにゴム厚と層数を決定すれば良いことになる。
積層ゴムの水平剛性の低下を10%以下とするためには、1次形状係数は次式を満足する必要がある。また、積層ゴムの製作精度を考慮して、$\small S_1\leq 40$程度がゴム層の厚さの限界ではないかと思われる。
$$S_1\geq\frac{3\sigma}{GS_2} \tag{7}$$
中間鋼板の厚さ$\small t_S$は、現在の製品では、$\small t_S/t_R\leq0.5$程度であり、$\small t_S=2~4mm$程度である。せん断変形時には中間鋼板は面外変形を起こす。特に反力中心の直下の中間鋼板と中心孔の周辺では塑性化する可能性が高い。よって、面圧が高い場合には、$\small t_S/t_R\geq0.75$程度とするなど、中間鋼板をより厚くすることが望ましい。
⑨ダンパーの設計
ダンパーがアイソレータ(積層ゴム)と別に設置される場合には、積層ゴムの設計とダンパーの設計・配置は別に実施できる。すなわち、ダンパーの総量は設計しようとしている建物に要求される減衰量を満足するようなダンパーの種類と個数を配置することになる。
履歴型ダンパー(高減衰ゴム系積層ゴムも復元力モデルは弾塑性型であり、同様に取り扱える)の場合、ダンパーの降伏せん断力係数$\small \alpha_S$は、0.03~0.05程度をなることが多い。
ダンパーには地震エネルギーの吸収のほかに、強風時に免震層が大きく変形しないような拘束効果も求められる。風荷重に対してダンパーの変形が弾性範囲であれば問題はないが、塑性化を許容する場合には、長時間にわたる繰り返し変形に対する安全性を検討する必要がある。また、風荷重に対するダンパー復元力のモデル化では、風荷重による変形が小変形であること、オフセット変形をした状態からの繰り返し変形となることなどを考慮すべきであり、地震荷重用の復元力モデルをそのまま適用できるか否かについては慎重に検討すべきである。住宅などのように上部構造が軽量の場合には地震荷重よりも風荷重の方が大きくなるため、ダンパーとは別にストッパーを設けることも多い。
⑩免震部材まわりの設計
アイソレータやダンパーが取り付く柱や基礎構造には、水平変形に伴ってせん断力が生じることになり、軸力とせん断力を適切に伝達できるようにしなければならない。加えてアイソレータの場合には、所定の軸力を支持しておりせん断変形にともなって偏心による曲げモーメントが加わることになる。偏心曲げモーメントは次式となる。
$$M=\frac{P\delta}{2}+QH \tag{8}$$
ここで、$\small P$:柱軸力、$\small Q$:積層ゴムのせん断力、$\small \delta$:水平変形量、$\small H$:積層ゴム中心からの高さ
この曲げモーメントによりアイソレータに大きな曲げ変形が生じないような曲げ剛性も躯体側に要求される。通常は積層ゴムの上下の梁、柱および杭で処理することになる。
⑪免震部材の配置
積層ゴム(アイソレータ)は柱下に1体設置する。もし、柱軸力が大きく、積層ゴムの直径が過大になるような場合には、柱下に2体以上のアイソレータを設置する。アイソレータのサイズが大きくなるとメーカーが所有している試験装置では製品性能の十分な評価が難しくなる。そこで、品質を確認できるサイズ、実績が豊富な製品サイズを選択することが免震建物としての品質を確保するには有効である。
ダンパーの配置にあたっては免震層の捩れが起きにくいように、すなわち免震層の剛心と上部建物の重心が一致するようにする。ダンパーが降伏すると免震層の剛性が変化するが、その場合でもできるだけ剛心と重心が大きく離れないことがねじれ応答が大きくならないために重要である。
ダンパー機能を有する鉛プラグ型積層ゴムやすべり支承などを使用する場合には、支承(ダンパー)の位置が柱の位置に固定されるため、重心と剛心をあわせるための調整が複雑である。
以上より免震層の設計は完成する。使用する免震部材・装置により多少の違いがあると思われる。しかし、基本的な考えは同じである。使用する免震部材の特性、限界状態を正確に把握し、免震部材に作用する荷重・変形などを予想し、それに伴う免震部材の特性変化の程度を確認した上で設計や解析に反映させることが肝要となる。加えて、免震部材のモデル化(剛性や降伏耐力など)が設計や解析にとって十分な精度と妥当性を有していることを確認することが大切である。
簡単な例題
ここでは、RC造9階建ての共同住宅を想定して、免震層(積層ゴム)の設計を行ってみる。建物の総重量は60,000kNで、各柱の軸力は下図のとおりとする。
設計変位を40cmと想定すると、③より積層ゴムの最小径は80cmとなる。そうすると最大面圧は15MPaで収まり、免震周期は(5)(6)式より4.4秒($\small S_2$=5、$\small G$=0.4MPa)と求められる。
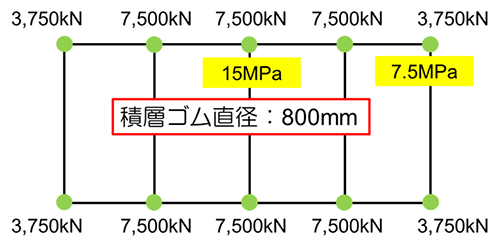
設計変位にもっと余裕を持たせたいと考え、積層ゴムの直径を1mと大きくした場合には、下図のようになる。この場合の免震周期は、3.9秒となる。
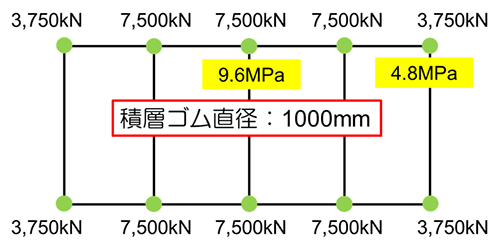
上図の天然ゴム系積層ゴムのうち6台を鉛プラグ入り積層ゴム(LRB)に置換してみる。鉛プラグの直径はいくつかのバリエーションが製品化されているが、ここでは積層ゴム直径の1/5だとする。鉛プラグの降伏応力度は約8.5N/mm²なので、降伏荷重は1台あたり267kNとなり、免震層全体での降伏荷重は約1600kNとなる。これは建物総重量の約2.7%に相当する。このダンパー量で地震時の応答変形、あるいは強風時の応答などで不足するということであれば、別途ダンパーを追加する、あるいは全てを鉛プラグ入り積層ゴムに置き換えることを検討することになる。
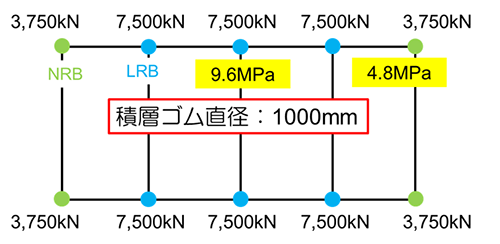
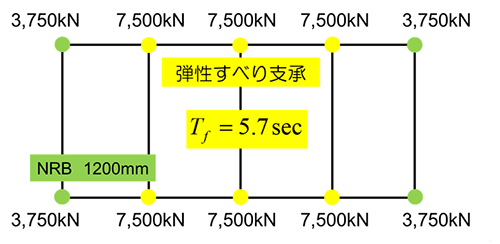
鉛プラグ入り積層ゴムではなく、弾性すべり支承を使うということも考えられる。上の図のLRB6台を弾性すべり支承に置き換えたとする。弾性すべり支承の摩擦係数が0.04だとすれば、免震層全体でのすべり荷重は1800kNとなり、建物総重量の3%となる。弾性すべり支承が滑っているときには、剛性を持たないので、積層ゴムの直径を1.2mと大きくしたとしても免震周期は5.7秒まで伸ばすことができる。ただし、弾性すべり支承の摩擦係数は面圧や速度による依存性があり、地震時の軸力変動による摩擦力の変動、すなわち減衰力の変動の影響を考慮することが必要となる。
ここで示した例題は非常に単純な平面形であり、偏心もない。実際には不整形な平面形の場合には、偏心に対する配慮も求められる。アイソレータやダンパーの選択と配置にあたってはさまざまな角度から検討することが必要だろう。そのためには、アイソレータやダンパーなどの免震部材の特性について、十分な知識が不可欠となる。
>> 「第4回:熊本地震における建築物の被害」