
石山 祐二
(いしやま ゆうじ
/ Yuji Ishiyama)
北海道大学名誉教授
(株)NewsT研究所代表取締役
< 略 歴 >
| 1942 |
北海道札幌市生まれ |
| 1965 |
北海道大学工学部建築工学科 卒業 |
| 1967 |
北海道大学大学院工学研究科 修士課程修了 |
1967
|
1971 |
建設省営繕局建築課 |
1971
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1991 |
建設省建築研究所
| 1982 |
工学博士(北海道大学) |
1984
|
|
|
1985 |
カナダ国立研究院建築研究所・客員研究員 |
1989
|
|
|
|
|
1991 |
ペルー国立工科大学、日本ペルー地震防災センター・チーフアドバイザー |
|
1991
|
|
|
|
1997 |
北海道大学工学部・教授
|
1997
|
|
2005 |
北海道大学大学院工学研究科・教授 |
| 2005 |
北海道大学定年退職・名誉教授 |
| 2005 |
日本データーサービス(株)・技術顧問 |
| 2005 |
日本建築学会賞(業績) |
| 2005 |
ペルー国立工科大学・名誉博士 |
| 2006 |
(株)NewsT研究所設立・代表取締役 |
| |
現在に至る |
6. 耐震規定の将来展望とコンピュータの活用
新耐震は手計算を前提として作成され、それに対し限界耐力計算は(計算式などから判断すると)コンピュータを用いることが前提となっている。
しかし、限界耐力計算は(コンピュータを用いることが前提になっている割りには)コンピュータの利点を十分生かした規定とはなっていない。
また、新耐震に基づく耐震計算ルート1~3の一貫計算プログラムも(そもそも新耐震は手計算を前提としているため)コンピュータの利点を十分活用していない。
コンピュータを用いることが前提ならば、それに適した規定・計算方法があるはずで、その中で特に気になっている点を述べてみたい。
6.1 構造特性係数$\small D_s$と増分解析
耐震計算ルート3では、各層の必要保有水平耐力$\small Q_{un}$が$\small C_0 = 1.0$とした設計用層せん断力$\small Q_{ud}$に構造特性係数$\small D_s$と形状係数$\small F_{es}$を乗じた次式で与えられている。
$$Q_{un} = D_s F_{es} Q_{ud} \tag{1}$$
ここで、$\small D_s$は、(構造種別ごとに若干異なっているが)基本的には【表1】のように$\small D_s F_{es}$告示(昭55建告1792)で与えられている。
この表中の架構の性状と形式については、部材を細かくランク付けし、それらの耐力比から$\small D_s$を求めるようになっている。
このようなマトリックス状の表から$\small D_s$を求めるという規定は、新耐震が施行された当初の手計算で保有水平耐力を計算するための便法と考えるべきで、本来は大地震動を受けた際の建築物の弾塑性挙動から直接求めるべきである。
新耐震施行当初は、保有水平耐力を手計算で行うことも多かったが、今ではほぼすべてコンピュータを用いた増分解析によって行われている。
その結果得られる荷重変位関係は、例えば【図1】の曲線aのように求まり、計算上はいくらでも変位を大きくすることができ、荷重も少しづつ増加している場合が多い。
これは解析を簡便に行うために、部材が降伏してもその耐力は低下せず、逆に少しずつ増加するように仮定している場合が多いからである。
このような解析からは、(層間変形角があまり大きくはない時の)保有水平耐力を求めることができても、$\small D_s$を求めることはできない。
しかし、各部材の変形にともなう耐力低下を考慮するならば、荷重変位曲線は【図1】の曲線bや曲線cのように求まり、許容塑性率を�$\small \mu$とすると、例えばエネルギー一定則から次式によって$\small D_s$を求めることができる。
$$D_s = \frac{1}{\sqrt{2 \mu - 1}} \tag{2}$$
すなわち、建築物の(変形にともなう耐力低下を取り入れた)弾塑性挙動を適切に考慮した増分解析を行うならば、得られた荷重変位曲線から$\small D_s$を求めることができるはずである。
さらに、適切な外力分布を用いるならば$\small F_s$は(この影響は増分解析の中で考慮できるはずなので)不要となり、床ダイヤフラムの(弾塑性を含む)強度・剛性も取り入れた立体解析を行うならば、建築物の捩れ変形や吹き抜けの影響も考慮されるはずなので、$\small F_e$も不要になる可能性がある。
限界耐力計算においても、変形にともなう耐力低下を考慮する増分解析は必要であることはいうまでもない。
このようなことを考えると、($\small P-\Delta$効果、耐震診断の第2種構造要素の影響などを含む)変形にともなう耐力低下を考慮した増分解析が可能となる新しい立体弾塑性解析プログラムとそれを前提とした耐震規定が期待される。
また、【表1】のように現行の$\small D_s$は0.05刻みの値となっていることについて考えてみよう。
$\small C_0 = 1.0$を低減する係数としては、0.05刻みは工学的に十分細かな区分であるようにも思えるが、$\small D_s$の最低値の0.25から考えると、0.05は20%という大雑把な区分である。
部材ランクのごくわずかな違いによって$\small D_s$が変わり、それが必要保有水平耐力の20%にも影響するとは考えられない場合も多く、少なくとも現行の$\small D_s$が階段関数的に決められている点を連続的となるように改正すべきであろう。
もちろん、荷重変形曲線から$\small D_s$を算定する規定となるならば、このような問題点も同時に解決されることになる。
【表1】構造特性係数$\small D_s$
| 架構の性状 |
架構の形式 |
| ラーメン |
その他 |
耐力壁または筋かい |
| A |
塑性変形能力が特に高い |
0.3 |
0.35 |
0.4 |
| B |
塑性変形能力が高い |
0.35 |
0.4 |
0.45 |
| C |
耐力が急激に低下しない |
0.4 |
0.45 |
0.5 |
| D |
その他 |
0.45 |
0.5 |
0.55 |
SRC造とS造では0.05小さい値となっている。
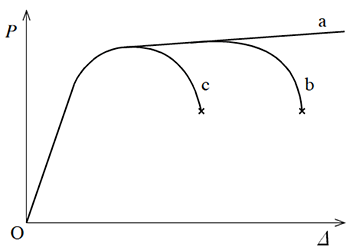
【図1】荷重変形関係
6.2 動的解析について
現行規定では、高さ60mを超える超高層建築物については動的解析を行うことになっているが、それ以外は動的解析がほとんど行われていない。
しかし、高性能のコンピュータと種々のソフトの普及を考えると、一般の建築物にも動的解析を行うことも考えた方がよいように思われる。
もっとも、将来起こるであろう地震動を完全に予測することは難しいので、動的解析のみで設計を行うのではなく、動的解析によってよりよい設計ができるようにするのがよいと考えている。
例えば、次のように(1)動的解析に基づく地震力を用いて設計し、その安全性を検証するために(2)時刻歴弾塑性応答解析をするのはいかがであろう。
(1)動的解析に基づく地震力(地震力の分布と形状係数)
動的解析結果を基に導かれた$\small A_i$分布は、通常の建築物に対してはほぼ適切な地震力の分布を与えるが、ツインタワー型の建築物、低層建築物上の塔状建築物、水平剛性の大きく異なる混合構造の建築物などについては動的解析(モード解析とスペクトル解析)を行い適切な地震力を与えて設計する。
また、立体解析を行うならば捩れ振動を含む適切な地震力を求めることができ、剛性率・偏心率を含む規定や形状係数の(現行規定の緩和を含む)適切な評価が可能となる。
(2)大地震動やそれを超える地震動を受けた場合の挙動解析
一般に構造設計では、ある目標を満足することを検証している。
例えば、中地震動($\small C_0 = 0.2$)に対して短期許容応力度を用い、大地震動($\small C_0 = 1.0$)に対して保有水平耐力を用いて検証する。
しかし、大地震動やそれを超える想定外の外力を受け、部分的な損傷が生じても、容易に全体崩壊につながらないこと(このような特性はロバスト性といわれる)を検証することも重要である。
このためにも、変形の増大にともなう耐力の低下はもちろんのこと、繰り返し荷重による耐力の低下、$\small P-\Delta$効果や柱が軸力を喪失した後の崩壊にいたるまでの挙動の解析可能な、かつ捩れ振動や上下振動も含む立体解析が可能であるコンピュータ・ソフトが開発されることを期待している。
参考文献
- 1)
- 石山祐二:「建築基準法の耐震・構造規定と構造力学」,三和書籍,2015.1
- 2)
- 石山祐二:種々の建物に対する地震層せん断力の分布とベースシヤー係数,日本建築学会構造系論文報告集,第439号,1992.9
以上でこのシリーズを終わります。
これまで目を通していただいた皆さんに感謝するとともに、建築構造に関する皆さんの日常業務、そして将来の耐震・構造規定に少しでも役立つならば幸甚です。