
|
- 第1回:流れの不思議(流体力学の基礎知識)
- 第2回:風はどのように吹いている?
- 第3回:強風災害から学ぶ
- 第4回:我が国における耐風設計の変遷
- 第5回:建築基準法の落とし穴-構造設計上の注意点-
- 第6回:低層建築物の耐風設計
|

植松 康
(うえまつ やすし
/ Yasushi Uematsu)
独立行政法人
国立高等専門学校機構
秋田工業高等専門学校
校長
- 1977年
- 東北大学工学部建築学科卒業
- 1982年
- 東北大学大学院工学研究科建築学専攻博士課程修了(工学博士)
- 1982年
- 東北大学工学部建築学科助手
- 1986年
- 東北工業大学非常勤講師
- 1994年
- 東北大学工学部建築学科助教授
- 1994年
- 東北工業大学大学院工学研究科非常勤講師
- 1998年
- 八戸工業大学非常勤講師
- 2002年
- コンコルディア大学(カナダ)客員教授
- 2003年
- 東北大学大学院工学研究科都市・建築学専攻教授
2019年4月 東北大学名誉教授
他に東北大学未来科学技術共同研究センター教授、東北大学大学院工学研究科副研究科長(総務担当)、宮城学院女子大学非常勤講師、哈爾浜工業大学(中国) Overseas Part-time Doctoral Co-supervisor、東北大学未来科学技術共同研究センター副センター長、中華人民共和国交通運輸部天津水運工程科学研究,Distinguished Expert and Chief Advisor (part-time)を歴任
■受賞歴
2005年5月
日本風工学会賞(論文賞)「独立上屋の風荷重に関する研究」
2009年3月
第20回風工学シンポジウム 論文賞 「機械的固定工法シート防水システムの疲労損傷を考慮した耐風性能評価法」
2010年8月
農業施設学会 論文賞 「園芸用パイプハウスの構造骨組用風荷重に関する研究-閉鎖型構造の外圧係数について-」
2014年5月
日本膜構造協会 膜構造研究論文特別賞
2019年5月
日本風工学会ベストペーパー賞 「変動風力を受ける円筒形貯槽の動的座屈特性」
2019年9月
日本農業施設学会 論文賞 「園芸用パイプハウスの風荷重による崩壊過程と補強効果の三次元解析による検討」
■専門
建築構造(特に建築風工学,鉄骨構造)
■学協会等の活動
日本建築学会 構造本委員会委員,荷重運営委員会委員,風荷重小委員会主査
日本風工学会 理事(会長),運営・学術委員長,風災害調査連絡委員会委員長
日本雪工学会 理事(会長),総務委員長
日本鋼構造協会 鋼構造と風小委員会委員長
その他の所属学協会 日本自然災害学会,農業施設学会,日本膜構造協会
国際風工学会(International Association for Wind Engineering)のアジア・オセアニア地区代表
■主な著書(いずれも共著)
シェル・単層ラチス構造の振動解析-地震、風応答と動的安定- 日本建築学会 1993年8月
動的外乱に対する設計-現状と展望- 日本建築学会 1999年5月
風工学ハンドブック―構造・防災・環境・エネルギー- 日本風工学会編 朝倉書店 2007年4月
容器構造設計指針・同解説 日本建築学会 2010年3月
WIND TUNNELS AND EXPERIMENTAL FLUID DYNAMICS RESEARCH, INTECH OPEN ACCESS PUBLISHER, 2011
ENVIRONMENT DISASTER LINKAGES, Community, Environment and Disaster Risk Management Vol. 9, Emerald, 2012
実務者のための建築物外装材耐風設計マニュアル 日本建築学会 2013年2月
建築物荷重指針・同解説 日本建築学会 2015年2月
建築物荷重指針を活かす設計資料集2 日本建築学会 2017年2月
第1回:流れの不思議(流体力学の基礎知識)
はじめに
2018年9月非常に強い勢力で徳島県に上陸し、大阪をはじめ近畿地方に甚大な被害をもたらした台風21号、2019年9月房総半島を襲った台風15号(令和元年房総半島台風)など、近年大型台風による強風被害が多発しています。地球温暖化により強大な台風の発生頻度の増大も予測されています。このシリーズでは、強風に対して安全な建築物・構造物を設計するにはどのような点に注意が必要かという観点に立ち、建築物の耐風設計の基礎知識について6回に分けて解説します。これをきっかけに建築物の耐風設計の重要性を再認識して頂けたら幸いです。
流体の運動
自然界にある物体は大きく「固体」、「液体」、「気体」の3つに分類されます。固体は、文字通り「固い」もの、すなわち、鋼やコンクリートのように、ちょっとやそっとの力では殆ど変形しないものです。これらはある状態下で一定の形を保持します。力を加えると、弾性範囲内であれば変形した状態で静止し、内部には法線方向の垂直応力度と接線方向のせん断応力度の両方が作用しますが、力を取り除けば元の形に戻ります。一方、液体と気体では、静止時には法線方向の応力(圧力)のみが作用します。ごく僅かな力でも作用させれば自由に変形し、どんなに大きな変形でも起こせます。力が作用しなくなれば静止しますが、決して元の状態に戻ることはありません。液体と気体は、このような共通の性質をもっているため、まとめて「流体」と呼ばれます。同じ流体でも、例えば水や油の場合には、一定の形をもたず、それを入れる容器次第でどんな形にもなりますが、体積は概ね一定に保たれます。このように容易に変形はするけど体積変化がほとんどないものが「液体」です。それに対して、空気のように形はもちろん体積も容易に変化することができるのが「気体」です。
私たちのまわりにある空気はいろいろな力を受けて運動します。それが風です。実際にどのような力が働いてどのような運動をするのか、また、気流中の物体がどのような力を受けるのかを知ることは、建築物・構造物の耐風性を論じる上で重要です。
レイノルズ数
空気を含め、流体は粘性や圧縮性など様々な性質をもっています。空気の流れにおいて圧縮性が問題になるのは、流速が音速に近いかそれを超えるような場合であり、耐風設計で対象とするような流れでは非圧縮性(密度$\small \rho$が一定)とみなすことができます。運動している流体に作用している力としては、①慣性力、②粘性力、③圧力勾配による力、④物体力(重力等)の4つが挙げられます。物体力は液体の流れにおいては重要な働きをしますが、気体の場合にはその影響を無視することができます。流体の運動で特に重要なのが慣性力と粘性力で、両者の比は流体の運動において重要な役割を果たします。代表寸法を$\small L$、代表速度を$\small U$とすると、慣性力$\small F_i$はニュートンの第二法則より、
$$F_i=(質量) \times (加速度) \propto (\rho L^3) \times \frac{U^2}{L}=\rho L^2 U^2 \tag{1.1}$$
一方、粘性力は流体に作用するせん断応力度$\small \tau$に起因します。ニュートン流体の場合、せん断応力度は流体の粘性係数$\small \mu$とせん断変形速度$\small (dU/dy)$の積で与えらますから、運動している流体に働く粘性力$\small F_v$は、
$$F_v=(せん断応力度) \times (面積) \propto \left( \mu \frac{dU}{dy} \right) \times L^2 \propto \mu \frac{U}{L} \times L^2 = \mu UL \tag{1.2}$$
ここで$\small F_i$と$\small F_v$の比をとってみると、
$$\frac{F_i}{F_v} \propto \frac{\rho U^2 L^2}{\mu UL}= \frac{\rho UL}{\mu}= \frac{UL}{v}=Re \tag{1.3}$$
ここに、$\small Re$は「レイノルズ数」と呼ばれる無次元量です。また、$\small v$は$\small v=\mu / \rho$で定義される「動粘性係数」です。$\small Re$が等しい場合には、物体の寸法が違っても、また、流体の種類が違っても流れは完全に相似となります。
完全流体の力学
強風中の構造物の$\small Re$は102~108のオーダーになります。高レイノルズ数流れとは粘性力に対して慣性力が非常に大きい流れを意味します。そこで1つの極限として粘性を無視した流体($\small Re= \infty$)を考えます。これを「完全流体」あるいは「理想流体」と呼んでいます。流れが定常ならば、ある1つの流線に沿って、次の「ベルヌーイの式」が成り立つことが知られています。
$$P+ \frac{1}{2} \rho U^2=一定 \tag{1.4}$$
ここで、$\small P$は流体の圧力を表します。また、物体力は変化が小さいとしてここでは無視しています(厳密には、右辺の「一定」に含まれています)。上式の物理的意味は、流線に沿って圧力と流体の単位体積当りの運動エネルギーの和が一定に保たれること、すなわち「エネルギー保存則」です。
風圧係数
流れの中に物体を置くと、【図1.1】に示すように、流れは物体前面上のある点(「よどみ点」)で堰き止められ、そこから両側に分れます。流速が0となるよどみ点を通る流線にベルヌーイの定理を適用すると、よどみ点の圧力$\small P_0$は、
$$\small P_0 = P_\infty + \frac{1}{2} \rho U_\infty~2 \tag{1.5}$$
ここに、$\small P_\infty$および$\small U_\infty$は物体の影響のない無限遠前方における流体の圧力および速度を表し、$\small P_\infty$を「静圧」、$\small q_\infty =1/2 \rho U_\infty^2$を「速度圧」あるいは「動圧」、$\small P_0$を「総圧」と呼びます。よどみ点の両側で分れた流線上の流速は物体の存在のため$\small U_\infty$とは異なる値$\small U$となり、再びベルヌーイの式を適用すれば、
$$\Delta P=P-P_\infty=\frac{1}{2}\rho(U_\infty^2-U^2)\tag{1.6}$$
なる圧力変化が生じ、これを「流体圧」(風の場合「風圧」)と呼びます。減速領域($\small U\lt U_\infty$)では静圧に対して圧力の増加(正圧)が、増速領域($\small U\gt U_\infty$)では、圧力の減少(負圧)が生じることになります。
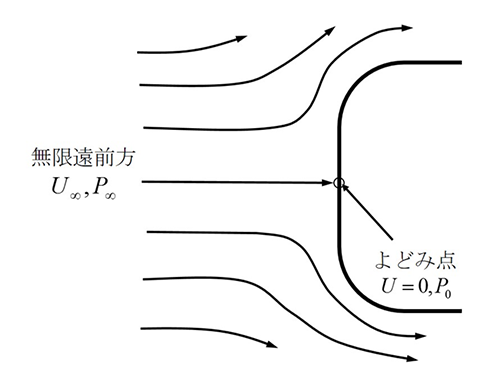
【図1.1】物体前方の流線とよどみ点
建築物の設計では、(1.6)式で与えられる圧力差$\small \Delta P$と$\small q_\infty$との比で定義される「風圧係数」$\small C_p$が風荷重計算に用いられます。
$$C_p=\frac{P-P_\infty}{q_\infty}\tag{1.7}$$
ダランベールのパラドックス
完全流体の中に置かれた二次元円柱の場合、円柱表面上の速度と圧力の分布は【図1.2】のようになります。圧力分布は左右、上下両方向に対称となっていますから、圧力の流れ方向および流れ直交方向成分を積分して得られる「抗力」および「揚力」はいずれも0になります。つまり、円柱には流体力が全く作用しないという、明らかに実験事実に矛盾する結果がもたらされます。これは「ダランベールのパラドックス」と呼ばれています。このような矛盾が生じたのは、流体が本来もっている粘性を無視したためです。
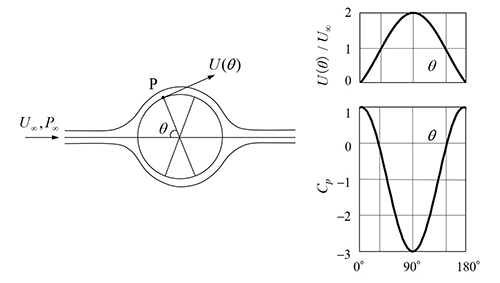
【図1.2】完全流体の中に置かれた二次元円柱表面の速度と圧力分布
二次元円柱まわりの粘性流れ
完全流体の場合には粘性がないので、円柱表面が1つの流線となり表面に沿う流れが発生します。しかし、実際の流体では多少なりとも粘性がありますので、物体表面上では流速は0で、外側に向かって流速が急激に変化する薄い層(境界層)が存在します。この境界層内ではせん断変形が大きいので、(1.2)式から推察されるように、物体表面には摩擦応力が作用します。この摩擦力によって側面のある点(「剥離点」と呼ばれます)で境界層が剥れてしまいます。
耐風設計で対象となる$\small Re$は、一般に104以上と大きくなります。【図1.3】1.1)は、抗力係数$\small C_D$の$\small R_e$による変化を実験で調べた結果の例ですが、$\small R_e$によって$\small C_D$が大きく変化することが分ります。これは流れの剥離点が$\small R_e$によって大きく変化するためです。図に示したように、円柱まわりの流れは、「亜臨界域」、「臨界域」、「超臨界域」、「極超臨界域」、4つのレイノルズ数領域に大別されます。各領域における流れの様子を模式的に描いたものが【図1.4】です。亜臨界域では、層流状態の境界層が風上よどみ点からの角度$\small \theta \approx 80^\circ \sim 90^\circ$で剥離(層流剥離:$\small LS$)します。超臨界域では、$\small \theta \approx 80^\circ$で層流剥離した流れが乱流に遷移($\small TT$)したあと円柱表面に再付着し、乱流境界層が生成されます。その乱流境界層が$\small \theta \approx 130^\circ \sim 140^\circ$で再び剥離(乱流剥離:$\small TS$)します。極超臨界域では、円柱表面に沿う境界層が乱流境界層となり、$\small \theta \approx 110^\circ$で剥離($\small TS$)します。臨界域は亜臨界状態から超臨界状態に遷移する中間の領域で、非常に複雑な性状を示します。特に興味深いのは、臨界域の中の狭いレイノルズ数範囲(【図1.3】中の〇の部分)で、【図1.4(b)】に示すように亜臨界域と超臨界域の両方の流れが同時に発生して、時間平均流れでさえ非対称になることです。空間的に一様な流れの中に点対称な断面形状の物体が置かれているのですから、時間平均流れは対称になるのが当たり前のように思われますが、実際には予想に反してこのような非対称な流れが発生するのです。ただし、気流の乱れが大きい場合や円柱表面が粗い場合には発生しません。
最も単純な一様流中に幾何学的に最も単純な円柱が置かれているのですから、流れの現象も単純だと思われますが、実際には上述のように非常に複雑な現象が発生するのです。そこが流体力学の難しいところでもあり、面白いところでもあります。
なお、建築分野で扱う構造物では、矩形のような鋭角をもった形状がほとんどです。そのような形状の場合、剥離点は$\small Re$によらず角部に固定されていますので、流れパターンは$\small Re$によってほとんど変化しません。したがって、実際より2桁小さい$\small Re$数での風洞実験の結果が実際の建築物・構造物の設計に利用できるのです。一方、曲面をもつ建築物・構造物の場合には、$\small Re$によって流れパターンが変化するので注意が必要です。そのような場合には、模型表面に粗度をつけたりして高レイノルズ数流れを再現する等の工夫がなされています。
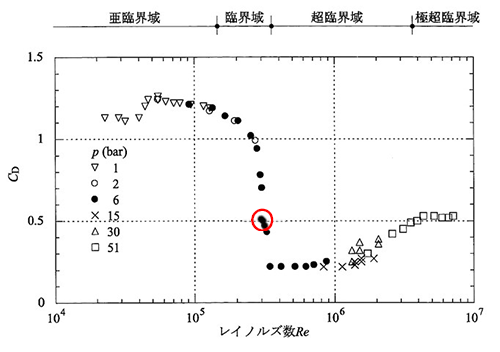
【図1.3】レイノルズ数$\small Re$による二次元円柱の抗力係数$\small C_D$の変化(文献1.1)のFig. 2(c)を加筆・修正したもので、日本建築学会「建築物荷重指針・同解説(2015)」より引用)
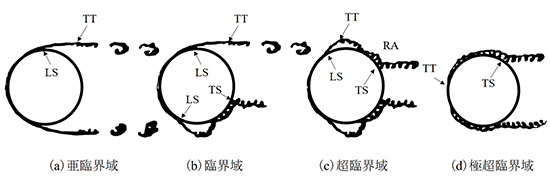
【図1.4】レイノルズ数による二次元円柱まわりの流れパターンの変化(文献1.2)の図11を参考に作成)
参考文献
- 1.1)
- Schewe, G. : On the force fluctuations acting on a circular cylinder in crossflow from subcritical up to transcritical Reynolds number, Journal of Fluid Mechanics, Vol.133, pp.265-285, 1983.
- 1.2)
- 松井辰彌 : 円柱を過ぎる流れの剥離、日本航空宇宙学会誌、第20巻、第226号、1972.