
石山 祐二
(いしやま ゆうじ
/ Yuji Ishiyama)
北海道大学名誉教授
(株)NewsT研究所代表取締役
< 略 歴 >
| 1942 |
北海道札幌市生まれ |
| 1965 |
北海道大学工学部建築工学科 卒業 |
| 1967 |
北海道大学大学院工学研究科 修士課程修了 |
1967
|
1971 |
建設省営繕局建築課 |
1971
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1991 |
建設省建築研究所
| 1982 |
工学博士(北海道大学) |
1984
|
|
|
1985 |
カナダ国立研究院建築研究所・客員研究員 |
1989
|
|
|
|
|
1991 |
ペルー国立工科大学、日本ペルー地震防災センター・チーフアドバイザー |
|
1991
|
|
|
|
1997 |
北海道大学工学部・教授
|
1997
|
|
2005 |
北海道大学大学院工学研究科・教授 |
| 2005 |
北海道大学定年退職・名誉教授 |
| 2005 |
日本データーサービス(株)・技術顧問 |
| 2005 |
日本建築学会賞(業績) |
| 2005 |
ペルー国立工科大学・名誉博士 |
| 2006 |
(株)NewsT研究所設立・代表取締役 |
| |
現在に至る |
2. 新耐震の地震力の与え方と $A_i$分布
2.1 地震層せん断力(係数)と水平震度
新耐震では、設計に用いる地震力を$\small i$階に作用する地震層せん断力$\small Q_i$として次式のように与えている。
$$Q_i=C_i W_i \tag{1}$$
ここで、$\small C_i$は次式で与えられる$\small i$階の地震層せん断力係数、$\small W_i$は$\small i$階より上の重量($\small i$階が支える重量)である。
$$C_i=Z R_t A_i C_0 \tag{2}$$
ここで、$\small Z$は地震地域係数、$\small R_t$は振動特性係数、$\small A_i$は地震層せん断力係数の分布係数($\small A_i$分布)、$\small C_0$は標準せん断力係数である。
$\small C_0$は中地震動で0.2、大地震動で1.0 である。
これらの値は、建築物の地表面に対する加速度応答倍率を2.5とすると、地表面加速度の重力加速度に対する割合(地盤震度)は中地震動で0.08、大地震動で0.4となる。
大地震動に対して弾性設計を行うことは(通常の建築物では経済的に)不可能に近い。
このため、建築物の構造的な粘り(靭性)に期待し、大地震動によって生ずる地震層せん断力$\small Q_{ud}$に構造特性係数$\small D_s$を乗じて低減し、構造的バランスが悪い場合は形状係数$\small F_{es}$を乗じて増加させ、必要保有水平耐力$\small Q_{un}$を次式のように与えている。
$$Q_{un}=D_s F_{es} Q_{ud} \tag{3}$$
新耐震以前に用いられていた震度$\small k_i$は、1階の地震層せん断力(ベースシヤ)$\small Q_1$を各階に分配し、それを$\small k_i$で表しているので、その階に生じる$\small Q_i$を表していない。
例えば、$\small Q_1$を頂部集中荷重として与え、最上階から最下階まで同一の地震層せん断力$\small Q_1$とする極端な場合を考えると、すべての階の$\small k_i$は0となるが、$\small k_i$が0であっても、その階に生じる$\small Q_i$は0ではない。
それに対し、$\small C_i$は(その階より上の部分の平均的な震度を表しているので)、その値のみで階の地震層せん断力$\small Q_i$の(それ以上の重量に対する割合としての)大きさを表しており、他の階の$\small C_i$や他の建築物の$\small C_i$と直接比較することができる。
このように、$\small k_i$と$\small C_i$は同じような意味を持っていて、$\small k_i$の方が分かり易いと感じるかも知れないが、非常に異なった面がある。
もっとも、(新耐震以前の高さ16mまでのように)最上階から最下階まで$\small k_i$が同一の場合は、$\small k_i=C_i$となるので、震度と層せん断力係数の区別をする必要がない。
次に示すが、$\small A_i$分布は層せん断力(係数)と基準化重量を導入したからこそ生まれた式である。
2.2 地震力の高さ方向の分布と $A_i$分布
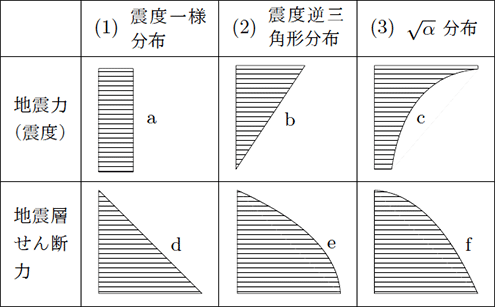
【図1】は地震力(震度)と地震層せん断力の典型的な分布を示している。
建築物が剛体として地面と水平方向に同一の動きをするならば、地震力(震度)は$\small a$のように建築物の上から下まで一様に分布し、これを(1)震度一様分布という。
建築物に生ずる地震力は上階から下階へ伝わり、最終的には地盤へと伝達される。
この伝達された地震力のある階までの和が地震層せん断力で、この場合は$\small d$のように上から下まで直線的に大きくなる。
建築物は剛体ではないので、上階の方が大きく揺れ、例えば震度がbのように作用すると、地震層せん断力はeのように(右に凸の)放物線で表される。
これを(2)震度逆三角形分布という。
超高層建築物は地震動を受けると最上部が鞭の先端のように大きく揺れる鞭振り現象が生ずることがあり、これを震度で示したのがcで、この場合の地震層せん断力はfのように(上に凸の)放物線で表される。
基準化重量を$\alpha$とすると、この放物線は$\small \sqrt{\alpha}$で表されるので、この分布を$\small \sqrt{\alpha}$分布と呼ぶことにする。
この分布はホワイトノイズを受ける基礎固定一様せん断棒の応答として理論的に求められる。
なお、cの震度は$\small 1/(2\sqrt{\alpha})$で表される。
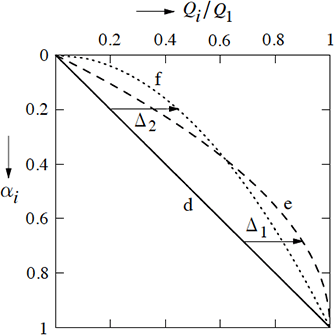
【図2】は【図1】の地震層せん断力d、e、f をまとめて示したもので、縦軸は基準化重量$\alpha_i$、横軸は地震層せん断力$\small Q_i$を最下層の地震層せん断力$\small Q_1$で除して基準化したもので、曲線eと直線aの差$\small \Delta_1$と曲線fと直線aの差$\small \Delta_2$を係数$\small k_1$と$\small k_2$を乗じて変化させると、種々の建築物に対する地震層せん断力の分布を次のように表すことができる。
$$\begin{align*}
Q_i/Q_1 & = \alpha_i+k_1\Delta_1+k_2\Delta_2 \\
& = \alpha_i+k_1(\alpha_i-{\alpha_1}^2)+k_2(\sqrt{\alpha_i}-\alpha_i)
\end{align*} \tag{4}$$
上式を$\alpha_i$で除すと($\small A_i$に相当する)地震層せん断力係数の分布係数$\small C_i/C_1$が次のように得られる。
$$C_i/C_1 = 1+k_1(1-\alpha_i)+k_2\left(\frac{1}{\sqrt{\alpha_i}}-1\right) \tag{5}$$
ここで、
$$k_1 = k_2 = \frac{2T}{1+3T} \tag{6}$$
とすると、次式の$\small A_i$分布が得られる。
$$A_i = 1+\left(\frac{1}{\sqrt{\alpha_i}}-\alpha_i\right)\frac{2T}{1+3T} \tag{7}$$
$\small A_i$分布は以上のようにして導かれたが、新耐震以前の旧規定との連続性を考え$\small T = 0$では震度一様分布になるように、かつ$\small T = \infty$の場合でも適用できるように$\small 2T/(1+3T)$の値が最小の0から最大で2/3となるようにした次第である。
なお、【図1】と【図2】に用いられている基準化重量$\alpha_i$は、各種の地震層せん断力(係数)や震度を比較したりするのに便利なパラメータで、$\small A_i$分布は地震力を地震層せん断力(係数)で表したことと$\alpha_i$をパラメータとしたから生まれた式である。
【図1】地震力(震度)と地震層せん断力の典型的な分布
【図2】3種類の基準化地震層せん断力 $\scriptsize Q_i/Q_1$
参考文献
- 1)
- 石山祐二:$\small A_i$分布の誕生とその経緯,日本建築学会大会学術講演梗概集(北陸)2092,1992.8
- 2)
- 石山祐二:種々の建物に対する地震層せん断力の分布とベースシヤー係数,日本建築学会構造系論文報告集,第439号,1992.9
>> 3.(耐震)壁を有効に活用しよう!