
石山 祐二
(いしやま ゆうじ
/ Yuji Ishiyama)
北海道大学名誉教授
(株)NewsT研究所代表取締役
< 略 歴 >
| 1942 |
北海道札幌市生まれ |
| 1965 |
北海道大学工学部建築工学科 卒業 |
| 1967 |
北海道大学大学院工学研究科 修士課程修了 |
1967
|
1971 |
建設省営繕局建築課 |
1971
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1991 |
建設省建築研究所
| 1982 |
工学博士(北海道大学) |
1984
|
|
|
1985 |
カナダ国立研究院建築研究所・客員研究員 |
1989
|
|
|
|
|
1991 |
ペルー国立工科大学、日本ペルー地震防災センター・チーフアドバイザー |
|
1991
|
|
|
|
1997 |
北海道大学工学部・教授
|
1997
|
|
2005 |
北海道大学大学院工学研究科・教授 |
| 2005 |
北海道大学定年退職・名誉教授 |
| 2005 |
日本データーサービス(株)・技術顧問 |
| 2005 |
日本建築学会賞(業績) |
| 2005 |
ペルー国立工科大学・名誉博士 |
| 2006 |
(株)NewsT研究所設立・代表取締役 |
| |
現在に至る |
4. 基礎と杭の緊結は不要!
最近では、基礎と杭の接合が強化される傾向にある。
しかし、この接合は過剰であるばかりか、建築物のみならず基礎や杭の地震被害を増大させる可能性が高いと考えられるので、次の2つの点から考えてみたい。
4.1 基礎・杭・地下部分の保有水平耐力計算は不要
新耐震以前では、水平震度0.2$\small Z$による短期許容応力度計算を行っていた。
しかし、このような建築物もたびたび地震被害を受けたため、大地震動に対する検討も行うことになり、(大規模な建築物には)保有水平耐力計算が導入された。
この保有水平耐力の計算は、当初から「地上部分」についてのみ行う規定となっている。
この理由は、過去の地震被害が地下部分まで及ぶことがほとんどなかったからで、これは地下部分には土圧・水圧に抵抗するため厚くて丈夫な壁が周囲に配置されており、この壁が耐震壁としても機能しているからである。
新耐震導入当時は、保有水平耐力の計算方法が確立しておらず、構造技術者にとってはなじみのない計算法であった。
また、コンピュータが十分普及していないこともあり、参考文献の解説書には「極限解析法や増分解析法等の清算によるほか、実用的には節点振り分け法や仮想仕事の原理を用いた方法を採用してよい。」と手計算が前提で書かれていた。
その他に、塔状比の大きな建築物では各階の水平耐力が大きくても、浮き上がりによって保有水平耐力が決まってしまう問題も議論された。
その結果、「梁間方向の短い壁式構造等のように、建築物全体の転倒モーメントによる浮き上がりによって耐力が支配される場合には、この浮き上がりがないものと仮定して崩壊メカニズムの形成を想定して差し支えない。」という解説があった。
これに対し、現行の平成19年国土交通省告示第594号(ルート1~3算定法告示)第4では、「・・・地盤、基礎杭、地盤アンカーはそれぞれの極限支持力を超えないこと。ただし、特別な調査研究によって・・・建築物の全体の転倒が生じないことを確かめた場合は、この限りではない。」という表現になっている。
最近は、保有水平耐力を計算するコンピュータ・ソフトが開発され、地上部分と地下部分を一体にモデル化し、$\small A_i$分布による水平力を用いた増分解析を行い、保有水平耐力を計算していることが多い。
このことは誤りではないが、保有水平耐力の計算が必要なのは地上部分のみで、地下部分や基礎・杭に適用する必要はない。
このことは、大地震動時に建築物の浮上がりや滑動を許容していると解釈することができるのに、上述の告示のただし書きより前の部分に従って、結局は浮き上がりが生じない耐力を保有水平耐力としていることも多い。
また、浮き上がりを阻止するために杭を用いたり、基礎と杭を緊結したり、基礎を地盤へ緊結するためアンカーを用いることもある。
しかし、建築物が転倒することは避けなければならないが、建築物は大地震動によって一時的に浮き上がっても転倒することはない(以前、参考文献のような「地震動による物体の転倒」の研究を行ったのは、建築物が地震動によって転倒する可能性を考えたかったからである)。
いずれにしても、現行規定では保有水平耐力の計算を地下部分・基礎・杭に行う必要はなく、浮き上がりによって保有水平耐力が決まってしまう場合は、1981年の解説のように、浮き上がりが生じないとして計算をして構わないと考えられる。
4.2 高次モードによる転倒モーメント(浮き上がり)は無視できる
耐震設計では、【図1a】のように地震力に相当する静的な水平力を考えるが、実際には地震力は動的に作用する。すなわち、地震時の建築物の振動は多くのモードが重なり、地震力は大きさも方向も時々刻々変動する。それを簡略化したのが【図1a】の設計用地震力である。
1次モードによる地震力は【図1b】のように建築物の上から下まで同じ向きに作用する(その大きさは時間的に変動し地震力が逆向きに作用することもある)が、高次モードでは【図1c】の2次モードのように地震力が上から下まで同じ向きに作用することはない。
建築物に作用する地震力は、すべてのモードが重なって生じるが、高次モードの地震力は(大きさや向きが変動しても)、【図1c】のように常に左右両方から作用するので、建築物の基礎の浮き上がりに直接影響する転倒モーメントを考えると、1次モードによる【図1b】の$\small M_1$に比べて【図1c】の$\small M_2$はほとんど0となり、一般に高次モードの転倒モーメントへの影響は無視できる。
$\small A_i$分布は各層に生じる地震層せん断力を計算するためのもので、$\small A_i$分布によって基礎に生ずる引張力や圧縮力を計算した場合には、高次モードの影響(1~2割程度)を減ずるべきである。
更に、基礎が浮き上がっても建築物が転倒することはないので、地震時に基礎の浮き上がりを許容した方が建築物への地震入力は小さくなり、基礎が地盤や杭の上で滑っても、それによって建築物への地震入力が低減されることになる。
以上のようなことから、基礎と杭の接合は、過剰であるばかりでなく、不要であり、場合によっては(基礎にも杭にも)危険側に作用するおそれがある。
耐震偽装事件以降の構造規定の改正により、建築物の構造性能が向上することよりも、計算上の偽装がし難いように計算方法を定めてしまったように思える。
構造技術者は、よりよい構造になるのであれば労力も時間も惜しまないであろうが、そうでなければ単に規定を満足する設計を行ってしまうであろう。
構造技術者の創意工夫によって、よりよい建築物ができるような規定となることを期待している。
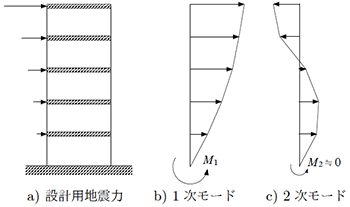
【図1】設計用地震力と振動モードによる地震力
参考文献
- 1)
- 建設省住宅局建築指導課・建設省建築研究所監修「構造計算指針・同解説」日本建築センター発行,1981.1
- 2)
- Ishiyama,Y.,"Criteria for Overturning of Bodies by Earthquake Excitations",日本建築学会論文報告集 第317号,1982.6
>> 5.限界耐力計算の地震力表示について