
石山 祐二
(いしやま ゆうじ
/ Yuji Ishiyama)
北海道大学名誉教授
(株)NewsT研究所代表取締役
< 略 歴 >
| 1942 |
北海道札幌市生まれ |
| 1965 |
北海道大学工学部建築工学科 卒業 |
| 1967 |
北海道大学大学院工学研究科 修士課程修了 |
1967
|
1971 |
建設省営繕局建築課 |
1971
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1991 |
建設省建築研究所
| 1982 |
工学博士(北海道大学) |
1984
|
|
|
1985 |
カナダ国立研究院建築研究所・客員研究員 |
1989
|
|
|
|
|
1991 |
ペルー国立工科大学、日本ペルー地震防災センター・チーフアドバイザー |
|
1991
|
|
|
|
1997 |
北海道大学工学部・教授
|
1997
|
|
2005 |
北海道大学大学院工学研究科・教授 |
| 2005 |
北海道大学定年退職・名誉教授 |
| 2005 |
日本データーサービス(株)・技術顧問 |
| 2005 |
日本建築学会賞(業績) |
| 2005 |
ペルー国立工科大学・名誉博士 |
| 2006 |
(株)NewsT研究所設立・代表取締役 |
| |
現在に至る |
5. 限界耐力計算の地震力表示について
限界耐力計算では、建築物の各階に作用する安全限界地震力を、【表1】に掲げる式によって計算した当該階以上の各階に水平方向に生ずる力の総和として計算することになっている。
【表1】に示された3つの式を比べてみるとすぐに分かるが、3つの式は加速度応答スペクトルに相当する部分を除き同一であるので、安全限界加速度応答スペクトルを$\small S_{As}$と表示して、【表2】のように表現すべきである。
【表2】の方が【表1】に比べて地震力がどのようにして与えられ、周期によって変化する部分は加速度応答スペクトルの部分のみであることなどが容易に理解できるであろう。
このようなことを考えずに施行令となってしまったのは誠に残念である。
なお、海外に日本の耐震規定を紹介する際には、私自身勝手に【表2】のように英訳している。
【表1】安全限界の各階の地震力(現行規定)
| $T_s < 0.16$ |
$P_{si} = (3.2+30T_s)m_i B_{si} F_\zeta Z G_s$ |
| $0.16 \leqq T_s < 0.64$ |
$P_{si} = 8m_i B_{si} F_\zeta Z G_s$ |
| $0.64 \leqq T_s$ |
$P_{si} = 5.12m_i B_{si} F_\zeta Z G_s/T_s$ |
- $T_s$
- 建築物の安全限界固有周期(s)
- $P_{si}$
- 各階に水平方向に生ずる力(kN)
- $m_i$
- 各階の質量(t)
- $B_{si}$
- 各階に生ずる加速度の分布を表す係数
- $F_\zeta$
- 振動の減衰による加速度の低減を表す係数※
- $Z$
- 地震地域係数
- $G_s$
- 表層地盤による加速度の増幅率
※ここでは減衰定数を表すのに$h$ではなく$\zeta$を用いる。
|
【表2】安全限界の各階の地震力(現行規定の修正案)
| $P_{si} = S_{As} m_i B_{si} F_\zeta Z G_s$ |
| 周期(s) |
安全限界加速度応答スペクトル $S_{As}$(m/s2) |
| $T_s < 0.16$ |
$(3.2+30T_s)$ |
| $0.16 \leqq T_s < 0.64$ |
$8$ |
| $0.64 \leqq T_s$ |
$5.12/T_s$ |
- $T_s$
- 建築物の安全限界固有周期(s)
- $P_{si}$
- 各階に水平方向に生ずる力(kN)
- $m_i$
- 各階の質量(t)
- $B_{si}$
- 各階に生ずる加速度の分布を表す係数
- $F_\zeta$
- 振動の減衰による加速度の低減を表す係数
- $Z$
- 地震地域係数
- $G_s$
- 表層地盤による加速度の増幅率
|
次に、質量と荷重について考えてみよう。
限界耐力計算では、地震力を求める際に用いる各階の質量$\small m_i$は「各階の荷重(各階の固定荷重及び積載荷重との和(・・・・・・多雪区域においては、更に積雪荷重を加えたもの・・・・・・)を重力加速度で除したもの)(単位 トン)」として規定されている。
一方、限界耐力計算と同時期にSI単位も導入され、固定荷重と積載荷重は1平方メートルにつきニュートンで与えられた表から算定することになり、荷重の単位はニュートンとなった。
すなわち、質量$\small m$、重力加速度$\small g$とすると、荷重$\small w$は$\small mg$として計算することになった。
しかし、地震力を求めるに際には、($\small mg$である)荷重$\small w$を求め、それを重力加速度$\small g$で除して質量$\small m$を求め、それに加速度$\small S_A$を乗じて地震力を求めていることになる。
すなわち、
$$地震力 = \frac{w}{g}S_A = \frac{(mg)}{g}S_A \tag{1}$$
しかし、上の(1)式は次の(2)式のように加速度を重力加速度で基準化しておくと、(重力加速度を乗じて得られている)荷重を重力加速度で除して質量を計算し、それに加速度を乗じて荷重とする余計な計算をする必要がない。
また、加速度を重力加速度で基準化すると荷重の単位にかかわらず式が成立するので、荷重の単位がニュートン、キロニュートン、ポンドやキロポンドでも成立する(計算間違いの少ない)式になるのである。
限界耐力計算に対するパブリックコメントを求めた際に示されていた建築基準法施行令改正(案)では単位が3桁も異なっていた。
人間である以上誤りを避けることができないが、このように1000倍もの誤りを(案)の段階とはいえ、見落としていたことの最大の原因は基準化が適切に行われていなかったからである。
$$地震力 = (mg) \left( \frac{S_A}{g} \right) = w \left( \frac{S_A}{g} \right) \tag{2}$$
【表3】安全限界地震層せん断力$\small Q_i$(地震層せん断力表示による新提案)
| $Q_i = C_i W_i$ $C_i = Z S_{A0} A_i F_\zeta G_s K_o$ |
| 周期(s) |
基準化加速度応答スペクトル $S_{A0}$ |
| $T_s < 0.16$ |
$(1+9.375T_s)$ |
| $0.16 \leqq T_s < 0.64$ |
$2.5$ |
| $0.64 \leqq T_s$ |
$1.6/T_s$ |
- $T_s$
- 建築物の安全限界固有周期(s)
- $W_i$
- $i$階より上の重量の和
- $A_i$
- 層せん断力係数の分布係数
- $F_\zeta$
- 振動の減衰による加速度の低減を表す係数
- $Z$
- 地震地域係数
- $G_s$
- 表層地盤による加速度の増幅率
- $K_0$
- 安全限界震度(=0.328)
|
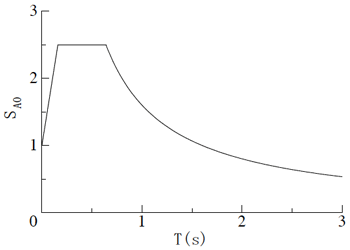
【図1】基準化加速度スペクトル $\small S_{A0}$
最後に、地震力の与え方について考えて見たい。
限界耐力計算では、「地震により建築物の各階に作用する地震力を、・・・・・・当該階以上の各階に水平方向に生ずる力の総和として計算すること。」といっているので、結局は地震層せん断力を用いている。
このため、各階の地震力ではなく、最初から地震層せん断力を与える方が分かり易い。
また、加速度応答スペクトルの形状は極稀地震も稀地震も同じなので、それを【図1】の基準化加速度応答スペクトル$\small S_{A0}$とし、加速度応答スペクトルの大きさを表すのに安全限界震度$\small K_0 = 0.328$とすると【表2】を更に発展させ【表3】のように表示することができる。
このようにすると、損傷限界には含まれていない係数を$\small F_\zeta = 1$、$\small G_s = 1$として、損傷限界震度を$\small K_0 = 0.0656$とすると損傷限界の地震力も算定できる。
また、限界耐力計算では$\small A_i$分布を変形した$\small B_i$分布を用いているが、この必要もなくなる。
何よりも重要なのは【表3】のように表示することによって、限界耐力計算では、地震力がどのように与えているかなどが明瞭になり、新耐震との比較も容易にできるようになる。
最近では、限界耐力計算がほとんど用いられていないようであるが、限界耐力のメリットが生かされるように改正され、用いられるようにと期待している。
参考文献
- 1)
- 石山祐二:建築構造を知るための基礎知識「耐震規定と構造動力学」,三和書籍,2008.3
>> 6.耐震規定の将来展望とコンピュータの活用