第3回：数値解析と図化の進化

AI（人工知能）と持て囃されても、その基本は17世紀の歯車手動の計算機と変わらず加減乗除の単なる四則演算をする事である。ただ2数間の大小の判別ができる事と演算速度が物凄く速く記憶も確かな点で、今、人間の歴史上初めて人智を越える物の出現として重視されている（【図14】）。

【図14】コンピュータの基本はあくまで四則演算（＋−×÷）であるが、数の大小が判別できる事と、何より、演算速度が早く記憶が確実で容量が膨大な事から多量の計算や試算が可能で、その点で人智を越える。

3. 数値解析

数値解析とは解析上の問題で、式の変換によって解を式として得る事が不可能な場合に、解を数値を用いて近似的に得る手法である。

例えば60進法使用の古代バビロンの粘度版では、ルート2を近似的に1+24/60+51/60²+10/60³として示していた。

3.1 四則演算への書き換え

例えば、【図15a】の用な関数$\small f\left(x\right)$で囲まれた部分の面積Aを求めるとすると、通常積分を使い

$$A=\int_{a}^{b}f\left(x\right)dx$$

とする。

コンピュータでも、コンパイラーを使いこれに似た表現で算定できるが、実際はコンピュータが、積分が判って式を変換し計算する例は稀で、人間が四則演算だけから構成される式に変えて計算を実行させている。例えば積分の代りに区分求積（【図15b】）とすれば、面積Aは四則演算だけで求められる。この時dを小さくとって計算回数を増やし精度を上げても、プログラム上も計算機に取っても全く支障がなく、通常必要とする精度は確保される。

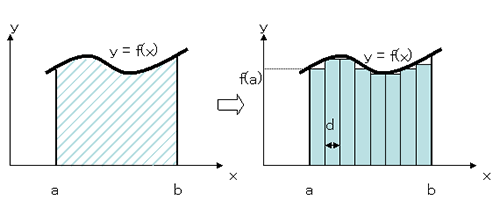
【図15a】例えば積分問題も四則演算に直す。

【図15b】区分求積なら積分によらず四則演算で積分と同等の計算ができる。精度を増す為にdを小さく取り計算回数を増やす事はコンピュータにとり全く問題ない。

しかしコンピュータには奥の手もある。乱数を利用して図上に点を打ちA部分にある点の数から面積を導き出す手法であり、人間が解析的に事象を掴めぬ場合、最後の手段としてこの『モンテカルロ法』に頼る事がある。多数量の計算を全く厭わないコンピュータの利用法の一つである（【図16】）。

【図16】先ず板に向かい銃を乱射する。次にある部分、例えばx=2,y=5で囲まれた矩形部分全部と面積を求めている
部分Aに当たっている弾数を数える。今、矩形部分に125個、内、求面積部分に21個当たっている。
だから、A=2x5x21/125=1.68（コンピュータでは銃の乱射の代りに乱数を発生させて計算します。）

3.2 数値解法の2法

数値解法には、主として直接解法と反復解法の2法がある。

直接解法では問題の解を有限個の計算で問題の解を得るが、一般に取り扱う数値の桁数に制限があるため近似解となる。例えば、多元連立1次方程式を解く場合、人間は、3元位迄は楽に解けるが、それ以上元数（即ち未知数）が多くなれば、時間が懸かり過ぎて解く気力を失う。しかしコンピュータでは遥かに元数の多い式を解き精度も必要に応じ高めることもできる。

反復解法では　反復回数をふやす事で正解に近づけるが、正解を得る前に反復計算を打ち切れば、やはり解は近似解となる。

例：問題　$\small 2x^3＋3＝19$を解く

直接解法：$\small x^3=(19-3)/2,\ x^3=8,\ x=2$

反復解法：$\small x=0$なら右辺$\small =3\lt19$,

$\small x+1$とし$\small x=1$に対し右辺$\small =5$，更に

$\small x+1$とし$\small x=2$に対し右辺$\small =19=19$で正解を得てOK

4. 図化

情報として伝えるにはデジタルの方が明確なので優れているが、人間はアナログの方が理解し易い事が多い。そこで初期に計算結果をプリンター上に図化するプログラムが簡単に作られた。それは、特筆する程の問題ではなかったが、次第に作図機に描く様に進化した。（以下、https://ja.wikipedia.org/wiki/プリンターを参考に記述）

4.1 プロッター

プリンターやプロッターは、コンピュータの情報出力装置として古くから利用されてきた。

プロッター（英：plotter）は、設計図面のような点や線を描くことを目的とした装置で、XとYの座標を指定して作図するので、「X-Yプロッター」とも言う（【図17】）。

プロッターは、時間がかかる、動作音が大きい、使用するペンの種類によってはペン先が磨耗して線幅が安定しない、といった欠点があった。プリンターの描画性能が劣っていた頃には、図面出力用機器の標準として使用されていたが、徐々に大型インクジェットプリンターなどに置き換えられ、現在では特殊な用途以外は使われなくなっている。

【図17】X-Yプロッター（今は殆ど使われていない）

4.2 プリンター

プリンターの印字方式としては、かつてはインパクト方式であるドットインパクトプリンターが主流であったが、1980年代から90年代を境にノンインパクト方式であるインクジェットプリンターやレーザープリンターなどが台頭、2008年当初ではパソコン用プリンター出荷台数の3分の2をインクジェットプリンターが占める様になった。

4.3 制御方式

1985年頃にセイコーエプソンの開発した制御方式、ESC/P（Epson Standard Code for Printer）は、仕様が公開されたため、他社のプリンターにも採用され、またAX（=Architecture extended）やDOS/V（DOS=Disk Operating System）ではプリンターの標準方式となっている。レーザープリンター用としては ESC/Pageがある。また、キヤノンが開発した制御方式にLIPSがあり、最新バージョンはLIPS Vである。

PostScriptは、米Adobe社が開発したページ記述言語で、テキストや図形の記述に人間が読むことの可能なASCII（=American Standard Code for Information Interchange）コードを使用することを基本とし、長い実績を持ち、特に高解像度が要求される印刷用のデータ処理では、圧倒的な支持を得ている。プリンターに対して文字の種類や印字位置をきめ細かく指定することが可能であり、また、プリンターごとの個別の機能や性能に依存しない出力が期待できるという利点がある。これによって、高品質な印刷が可能となり、仕上がりを確認した後に印刷業者の高解像度の出力機で大量印刷に回すといった流れが可能となった。2008年、PostScriptはページ記述言語の標準仕様となっており、Adobe Systemsによれば、欧米の商業印刷物の75%がAdobe PostScript技術を搭載した装置によって制作されているとされる。

（次回に続く）