第5回 長周期地震動と免震

はじめに

前回に引き続き、今回も免震にとって都合の悪い話になりそうです。

免震は長周期構造物ですから、長周期地震動では共振して大きな応答が生じるかもしれません。

長周期地震動は、免震にとって想定外の出来事なのでしょうか。

たとえそうであっても、とにかく安全であることを確認しなければなりません。

2003年十勝沖地震の影響

2003年9月26日午前4時50分に、十勝沖を震源とするマグニチュード8.0の地震が発生しました。

北海道の太平洋沿岸では最大で震度6弱を記録しました。

2003年十勝沖地震における免震のパフォーマンスは、第1回でご紹介した通りすばらしいものでした。

ところが、免震ではない構造物の被害から、免震が苦境に立たされることになりました。

苫小牧市内の石油タンクにおいて、液体のスロッシング現象が原因で大火災が発生したのです。

スロッシングは液面が振動で揺れる現象であり、これを引き起こしたのが震源からやってきた地震波です。

苫小牧市内の揺れは震度5弱でした。

しかし、それだけでは石油タンクの大火災に至らなかったはずです。

苫小牧市周辺の地下構造が長周期成分を増幅させてしまい、それが石油タンクのスロッシング周期と一致してしまったことが原因です。

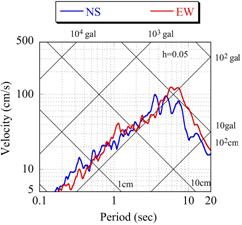
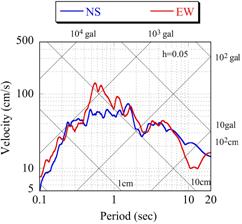
【図5.1】はK-NET苫小牧とK-NET釧路で観測された水平地震動成分の速度応答スペクトル（減衰定数5%）です。

K-NET苫小牧の応答スペクトルには、周期6～8秒の周期帯にピークが見られます。

一方、K-NET釧路の応答スペクトルにも同じ周期帯域に山が見られますが、他の帯域ほど増幅はされていません。

石油タンクの火災は、地震動そのものの周期特性と苫小牧市周辺の地下構造の増幅特性とが合わさって生じたと言えるでしょう。

この地震をきっかけとして長周期地震動が注目され、海溝型巨大地震による地震動に対する長周期構造物の安全性が懸念されるようになりました。

免震も例外ではありませんでした。

（a）K-NET 苫小牧	（b）K-NET 釧路
【図5.1 2003年十勝沖地震の応答スペクトル】

AIJ「東海地震等巨大災害への特別調査委員会」での検討

2003年十勝沖地震の被害がきっかけとなって、日本建築学会では「東海地震等巨大災害への特別調査委員会」が発足しました。

免震に関しては、建築構造物小委員会の下に免震建物WGが組織されて検討を行うことになりました。

免震建物WGでは、まず初めに長周期地震動に対して免震は安全なのか？という問いに対して、免震構造の極限事象の洗い出しから始まりました。

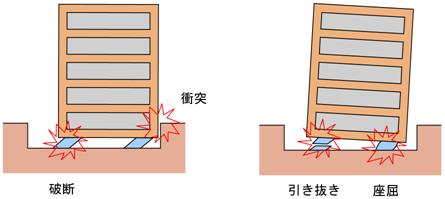
【図5.2】は想定した極限事象の一例です。

地震動チームの検討結果からは、長周期地震動は単に長周期成分が卓越しているだけではなく、継続時間が数分に渡るほど長くなることが指摘されました。

【図5.2】は一過性の事象ですが、その他に長時間の揺れを受けたときの免震装置の復元力特性劣化の問題も新たに浮上しました。

特別調査委員会での活動は、免震の問題点を再認識する意味において良い刺激となりました。

以下では、特別調査委員会での活動をきっかけとして始めた研究について紹介します。

【図5.2 長周期地震動下で想定される免震の極限事象】

積層ゴムの大変形モデル

【図5.2】に挙げた免震の極限事象は、いずれも積層ゴムが過大な変形を強いられることが原因です。

積層ゴムが単に過大な水平変形を生じるだけであれば、第2回でご紹介した復元力モデルを用いるだけで事は足ります。

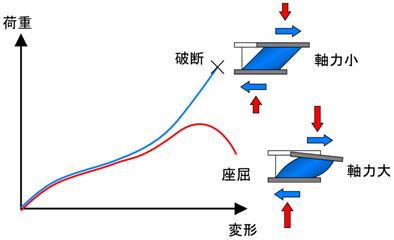
しかし、積層ゴムには【図5.3】のように軸力に依存してせん断特性が変化する性質があります。

この性質は、積層ゴムの2次形状係数（ゴム直径/ゴム層厚）が小さい場合や、軸力の変動が大きい場合に顕著に現れます。

できれば、そうならない範囲で使用したいものです。

【図5.3 軸力に依存して変化する積層ゴムの水平特性】

軸力とせん断の相互作用に問題に関しては、Kelly先生とKoh博士が1982年にTwo-springモデル^{参考文献5.2)}を提案されています。

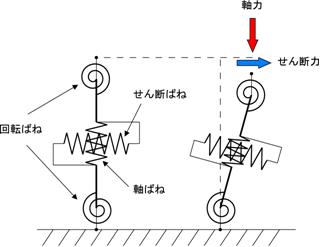
その後、このモデルは改良されて、【図5.4】のようなKoh-Kellyモデル^{参考文献5.3)}となっています。 Koh-Kellyモデルでは、せん断ばねの上下端に取り付いている回転ばねがせん断ばねを傾かせ、さらにリジッドリンクとP-Δ効果によって発生する曲げモーメントを考慮することで、軸力とせん断の相互作用を表現します。

当初、Koh-Kellyモデルは、ばねを線形として扱い、幾何学的非線形の影響を調べる目的で用いられました。

筆者は、Koh-Kellyモデルのせん断ばねと回転ばねに材料非線形性を与えることで、【図5.3】のような特性を表現可能であることを確認しました^{参考文献5.4)}。

せん断特性が同じであっても、回転ばねに与える非線形性によってハードニングや座屈の違いを表現することができるのです。

しかし、ここで新たな問題が生じました。

地震応答では軸力が刻々と変化します。

特に、建物端部に設置される積層ゴムにとっては、建物の転倒モーメントに起因する軸力変動が無視できなくなります。

軸力が変われば回転ばねに与える特性も変化させる必要がありますが、回転ばねの特性を軸力に応じて変化させることは困難です。

【図5.4 Koh-Kellyモデル】

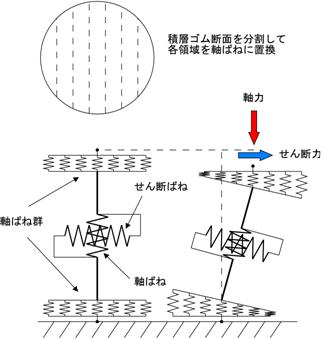
この問題を解決する方法として、【図5.5】のように回転ばねに代えて軸ばね群を上下端に取り付ける力学モデルを新たに考えました。

この力学モデルには並列軸ばねモデルという名称を与えました。

ちょうど柱部材の軸力と曲げの連成を考慮したMSモデルあるいはファイバーモデルと同じコンセプトです。

軸ばね群には、引張ではすぐに降伏し圧縮には非常に強いという引張と圧縮で非対称となる積層ゴムの特有の鉛直特性を与えます。

【図5.5 並列軸ばねモデル】

並列軸ばねモデルを用いて、鉛プラグ入り積層ゴムの加力試験結果をシミュレーション解析してみました。

試験では、軸力の影響が現れやすいように2次形状係数が4の試験体を用意しました。

免震建物の側柱下に設置されている積層ゴムの地震時の荷重状態を想定して、水平変形に連動させて軸力を変化させました。

右側に行くと軸力は小さくなり、左側へ行くと軸力は大きくなります。

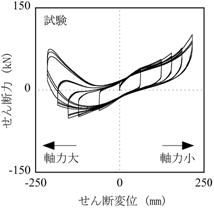
【図5.6】に検討結果を示します。

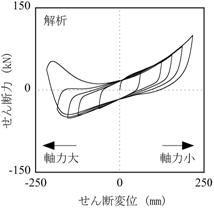
試験結果に見られる非対称な水平特性が、解析でも良好に表現されていることがわかります。

このように並列軸ばねモデルは、様々な面圧で変化する水平特性を荷重条件のみで再現することができます。

（a）試験結果	（b）解析結果
【図5.6 変動軸力試験結果とシミュレーション解析結果】

積層ゴムの特性劣化モデル

長周期地震動で問題となったもう一つが、長時間の繰り返し載荷です。

過大な変形でなくとも、長時間の多数繰り返し変形を受けると、免震装置の復元力特性が劣化するかもしれないという懸念が生じました。

どのように劣化するかと言えば、金属系のダンパーでは疲労破壊による破断ですし、支承減衰一体型積層ゴムでは減衰性能の低下です。

支承減衰一体型積層ゴムである鉛プラグ入り積層ゴムは、天然ゴム系積層ゴムの中心に鉛プラグを挿入した構造となっており、地震による運動エネルギーは鉛プラグの塑性変形によって吸収され、鉛プラグの発熱という形で熱エネルギーに変換されます。

ゴムは断熱性の高い材料であり発生した熱が内部にたまると、鉛プラグの温度が上昇して鉛の降伏点応力度を下げてしまいます。

その結果、履歴ループの面積が減少し、エネルギー吸収能力が低下してしまいます。

長周期地震動に長時間さらされると、この低下が無視できなくなる可能性があるのです。

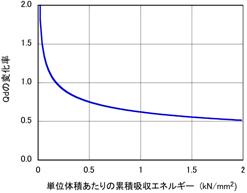
【図5.7】は、鉛プラグの単位体積あたりのエネルギー吸収量とQd（荷重切片）の変化率（設計値に対する変化）を調べた結果の一例です。

グラフの曲線は右下がりとなっていて、エネルギー吸収量が増加するとQdが下がる傾向を示しています。

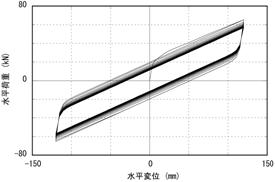
この関係を、第2回でご紹介した鉛プラグ入り積層ゴムの復元力モデルに適用してみたのが【図5.8】です。

実験でも概ね【図5.8】のような結果が得られているようです^{参考文献5.5)}。

今後、このモデルを用いて長周期地震動下での免震の応答特性を調べてみようと考えています。

【図5.7 エネルギー吸収量と荷重切片Qdの変化率の関係】

【図5.8 Qdの変化を考慮した荷重変形関係の再現】

おわりに

今回は、長周期地震動に対する取り組みについてお話しました。

最初に申し上げた長周期地震動下での免震の極限事象のうち、積層ゴムの過酷な状況（過大な水平変形、座屈、疲労劣化など）を考慮できる幾つかの方法をご紹介しました。

積層ゴムに長周期地震動下で想定される過酷な状況を与えることは、加力装置の能力の制限などから困難な場合が多々あります。

国内での試験が不可能なために、海外で試験を実施している例もあります^{参考文献5.6)}。

長周期地震動に対する免震の安全性の検証という課題への取り組みは始まったばかりであり、免震の一層の普及を図るには、避けて通れない課題です。

筆者もここで紹介した方法を活用して、免震の安全性を検証していきたいと考えています。

なお、【図5.1】では、防災科学技術研究所K-NETの強震記録を使用させていただきました。

ここに記して感謝の意を表します。

参考文献

5.1)

C. G. Koh, J. M. Kelly, A simple mechanical model for elastomeric bearings used in base isolation, International Journal of Mechanical Sciences 1988; 30: 933-943.

5.2)

James M. Kelly, Earthquake-resistant Design with Rubber (2nd edition). Springer: London, 1997.

5.3)

M. Kikuchi, S. Yamamoto, I. D. Aiken, ‘An analytical model for lead-rubber bearings under large deformations’, Proceedings of the 8th Pacific Conference on Earthquake Engineering, Singapore, No.222, 2007.

5.4)

Sachie Yamamoto, Masaru Kikuchi, Masaiki Ueda, Ian D. Aiken, ‘A mechanical model for elastomeric seismic isolation bearings including the influence of axial load’, Earthquake Engineering and Structural Dynamics, Vol. 38, 157-180, 2009.

5.5)

西澤崇雄・山本裕，川口澄夫，金子修平：鉛プラグ入り積層ゴムの繰り返し加振実験報告，日本建築学会大会学術講演梗概集B-2，pp.445-446，2004年

5.6)

嶺脇重雄，山本雅史，東野雅彦，浜口弘樹，久家英夫，曽根孝行，米田春美，和田章：超高層免震建物の地震応答を想定した実大免震支承部材の性能確認試験，構造工学論文集，Vol.55B，pp.469-477，2009年3月